Úloha na určení maxima
Dušan Polanský
Každý se baví jinak. Já občas i matematikou, ale nic vážně, spíš jenom lehce, a jenom tím, co mě zaujme. Proč také ne, když mě nečeká z tohoto předmětu povinná maturita! Což mezi námi děvčaty je pěkná pitomina, ale znáte to, lidí na vyšších postech rádi tropí hlouposti a navíc se nás přitom snaží přesvědčit, že mládeži chtějí jenom a jenom dobře. Takže nestrašme matematikou a raději si o něčem lehce nezávazně laicko-matematicky povídejme.
Dnešní povídání bude o hledání maxima. Ono vůbec matematika velice často řeší různé optimalizační úlohy, tedy úlohy o určení maxim a minim. Nakonec tak to chodí i v životě. Chceme ze života vydolovat maximum, ale přitom vydat minimum energie. Dopadně to ne vždy dobře, ale v matematice máme tu výhodu, že i když se k výsledku nedopracujeme, obvykle se nic neděje, tedy pokud nás zrovna nezkouší učitel. Jedno povídání o optimalizaci, přesněji o tzv. Bellmanově principu optimality, jsem již napsal, viz zde, tam jsme pomocí tohoto principu hledali minimální cestu. U Bellmana jsme si vystačili s učivem ze základní školy. Tentokráte použijeme středoškolskou matematiku, přesněji algebru, a budeme hledat největší pravoúhlou plochu, kterou lze nakreslit dovnitř kružnice. Jinak většina z vás výsledek, k jemuž se zde horko těžko dopracujeme, asi zná z geometrie. Nám ale ani tak nepůjde o výsledek, jako o ukázání postupu, jak se lze k takovému výsledku dopracovat. Současně se trochu potrénujeme v algebraických úpravách, protože někdy nestačí znát jenom postup výpočtu, ale potřebná je i počtářská zručnost, podobně jako je tomu u řemeslníka, ten musí mít zase šikovné ruce.
Pro znalé základů vysokoškolské matematiky, přesněji elementů diferenciálního počtu, úlohu vyřešíme i jinak, trochu elegantněji, právě pomocí diferenciálního počtu.
Obvykle se tahle častá školská úloha zadává nějak takto: máme kmen stromu, jehož nejmenší poloměr kolmého příčného řezu je r. Naším cílem je využít maximum dřeviny, což znamená, že z kmene máme vyříznout hranol, jenž bude mít v příčném řezu maximální plochu. Tedy máme spočíst rozměry příslušného pravoúhelníku. Trochu složitější zadání by bylo, kdybychom měli vyříznout hranol o maximální únosnosti na ohyb. My ale zůstaneme o jednoduššího případu, protože nám půjde hlavně o pochopení hlavní myšlenky a příslušných matematických postupů, jak se s takovou úlohou vypořádat.
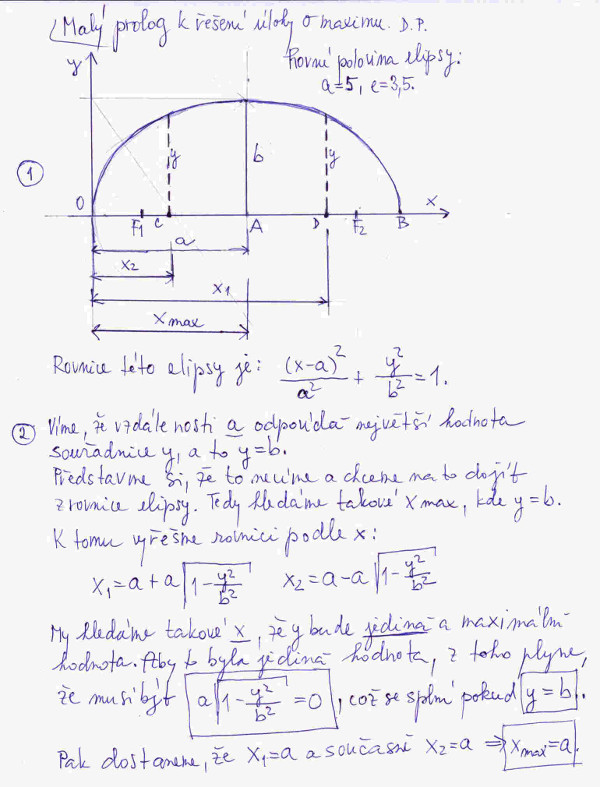
Než se do řešení pustíme, vysvětlíme si fintu, kterou použijeme při řešení bez znalosti diferenciálního počtu. O co jde, si vysvětlíme na obrázku č. 1; číslo obrázku zjistíte po najetí myši na obrázek. Na obrázku vidíme nakreslenou hornou polovinu elipsy. Její rovnice je uvedena pod obrázkem, pokud se vám nezdá, podívejte se na jedno možné odvození zde. Představme si, že nevíme, že největší hodnota ypsilonové souřadnice obvodu elipsy odpovídá na ose x vzdálenosti a. Měli bychom to dokázat z rovnice elipsy. Když je to správná rovnice, musí tam být o elipse vše, i to, co chceme teď zjistit. Uděláme to tak, že prvně rovnici elipsy vyřešíme pro x. Jelikož elipsa je křivka symetrická podélně i příčně, nějakému pevně zvolenému y, viz dvě čárkované čáry symetricky položené vůči středu, musí až na tři speciální případy – v bodech O, A a B – odpovídat vždy dvě nenulová řešení na ose x. Ale protože mi hledáme jedno jediné maximum, musíme se zbavit ve vzorcích pro x výrazu pod odmocninou, tedy tento výraz musí být roven nule, pak x1 i x2 nám dá stejný výsledek. Výrazy pod odmocninou budou nulové pro y = b, což jistě není náhoda, jelikož právě b je maximem. Tuhle fintu použijeme i při řešení naší úlohy.
Celý postup řešení naší úlohy bez využití diferenciálního počtu je uveden na obrázku č. 2. Jak vidíte postup je docela náročný na algebraické úpravy. Vidíme, že nám vyšlo, že hranol musí mít čtvercový profil, což jaksi víme již z geometrie.

Pokud známe základy diferenciálního počtu, tedy umíme alespoň trochu derivovat a je nám známo, že v místě maxima nebo minima musí být první derivace rovná nule, výpočet se zjednoduší. O tom, že jsme opravdu spočetli maximální plochu a ne minimální – z hlediska zadání naší úlohy to nemá smysl –, by nás přesvědčila zápornost druhé derivace, ale protože nám vyšel nenulový výsledek výpočet druhé derivace si odpustíme. V bodě č. 2 na obrázku č. 3 jsem pro ty, co jsou starší (asi jako já a více) a moc si již z matematiky nepamatují, připomenul dvě pravidla, které jsme pro výpočet derivace použili. Pochopitelně dopracovali jsem se k stejnému výsledku jako při prvním postupu.

Naše úloha je z těch jednodušších, proto jsem ji zvládli vyřešit i bez znalosti diferenciálního počtu, tedy pomocí středoškolské matematiky. Bohužel ne vždy to jde. Třebaže platí jedno, zdatný teoretik by měl umět hlavní myšlenku (pointu) řešení vysvětlit i bez složitého aparátu. Pokud to neumí, jednak problematiku do hloubky nepochopil, což je sice smutné, ale co je zásadnější, takový člověk by neměl matematiku učit. Takový učitel vám totiž matematiku jenom zhnusí.
V Brně 6. října 2019.