Odvození rovnice elipsy
Dušan Polanský
Tohle povídání jsem již poměrně dávno komusi slíbil. Jenom si pamatuji, že mi řekl, že na střední škole v matematice nikdy nepochopil, jak se odvodí rovnice nějaké křivky, např. elipsy. Popravdě se tomu ani moc nedivím, pokud si dobře vzpomínám, na střední škole nám učitel napsal na tabuli finální vzorec a šlus. Ono vůbec laici mají často před důkazy v matematice respekt, prý jsou těžké. Pravda to dost často je, ale je také jiná pravda, že důkaz vám nejednou pomůže ukázat a pochopit lépe hloubku toho, co se dokazuje.
Když jsem tohle povídání kdysi slíbil, hned na druhý den jsem si připravil v tužce koncept. Bohužel pak jsem na slib nějak zapomněl, koncept jsem kdesi založil, no a bylo nevymalováno. Teď jsem koncept zcela náhodou objevil, pochopitelně při hledání něčeho zcela jiného, což jsem ovšem nenašel. Slib alespoň opožděně plním, třebaže mi je jasné, že ten, komu jsem to slíbil, se o tom již nedoví. Odvození je trochu jiné, než se běžně vyskytuje v učebnicích analytické geometrie, ale kdyby trochu jiné nebylo, asi by ho nemělo smysl vůbec publikovat, stačilo by dát odkaz na vhodnou literaturu. Pokud jde o vstupní znalosti, vystačíme se znalostmi matematiky ze základní školy.
Provázková (zahradnická) konstrukce elipsy
Začneme coby zahradníci. Představme si, že máme za úkol na zahradě vysadit květinový záhon ve tvaru elipsy. Elipsa je křivka, jejíž horní polovinu vidíte na prvním obrázku. Číslo obrázku zjistíte po přesunu myši na obrázek. Jak takovou elipsu na zahradě nakreslíme? Především co budeme k tomu potřebovat? Odpověď zní: provázek, tři kolíky zašpičatělé na jednom konci a kladivo. Dále musíme vědět, jak má být elipsa dlouhá a vysoká a kde bude ležet její hlavní osa, což ale víme, jelikož jsme si předem ujasnili, kolik máme na elipsu místa a jak ji chceme mít umístěnou. Na obrázku je délka elipsy označena jako 2a (hlavní osa) a její výška 2b (vedlejší osa). Zatím si nevšímejte, že elipsa na obrázku, je nakreslena na základě znalosti veličin a a e, k tomu viz povídání o kus dále. My coby zahradníci budeme vycházet ze znalosti a a b. Obvykle tomu totiž při zahradničení tak je.
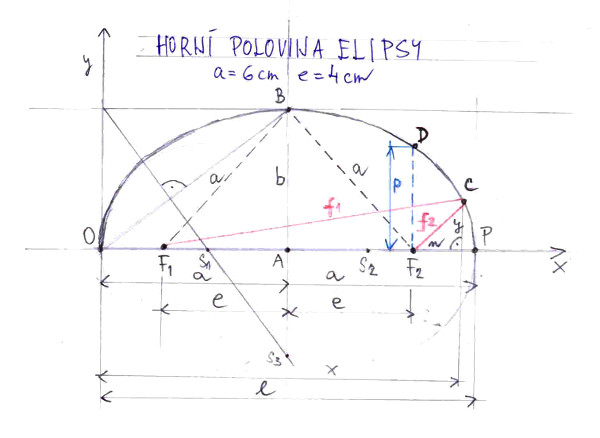
Najdeme si střed hlavní osy, na obrázku je označen A. V tomto bodě vztyčíme kolmici na hlavní osu, k tomu můžeme použít pravidlo třech délek: např. 3, 4 a 5 metrů (či jiných libovolných délek), což je rafinovaně vyslovena věta nějakého Pythagorase ze Samu, který zde pobýval přibližně 570 až 510 roků př. n. l. Na tuto kolmici, teda vedlejší osu, naneseme nad a pod hlavní osou délku b. V našem obrázku v horní polovině tomu odpovídá bod B. Z bodu B vyneseme délku a. Jak vyneseme, je zřejmé z čárkovaných čár. Pochopitelně provázek máme při této akci hezky napnutý. Tím dostaneme na hlavní ose body F1 a F2 (obvykle jim říkáme ohniska nebo fokusy). V bodech F1 a F2 zatlučeme do země kolíky. Na provázku si odměříme a označíme barevnou fixkou délku 2a a provázek uvážeme ke kolíkům v bodech F1 a F2 tak, aby délka provázku byla přesně 2a. A teď nás čeká nejtěžší akce. Třetím kolíkem (k tomu nic nepřivazujeme, je volný) napínáme provázek připevněný k bodům F1 a F2, přičemž dbáme, aby třetí kolik byl stále hezky kolmý k zemi, a špičkou kolíku kreslíme obvodovou křivku elipsy.
Na obrázku jste si jistě všimli třech bodů: S1, S2 a S3. Jsou vyloženě pomocné, slouží pouze a jen k nakreslení elipsy na mém obrázku, nemají nic společného s kreslením elipsy na naší fiktivní zahradě! Jsou to středy tzv. oskulačních kružnic. Z obrázku by mělo být zřejmé, jak se tyhle středy získají. Z těchto středů se nakreslí zmíněné oskulační kružnice; první má střed v bodě S1 a poloměr je S1O, druhá v bodě S2, poloměr je stejný jako u prvé, no a třetí kružnice má poloměr S3B. Problém je trochu v tom, že oblouky kružnic se nedotýkají. Řeší se to tak, že k plynulému přechodu z jedné kružnice do druhé se použije tzv. křivítko; různé typy se prodávají v papírnictví. Křivítko jsem doma neobjevil (ale někde určitě je), tak jsem přechod mezi kružnicemi nakreslil volně rukou.
Poznámka k veličinám a, b a e. Z obrázku je zřejmé, že jsou provázané vztahem e2 + b2 = a2. Z téhle provázanosti plyne, že k nakreslení elipsy musíme znát dvě z těchto veličin a třetí odvodíme z uvedeného vztahu. Nelze zvolit všechny tři zcela libovolně. Na naší zahradě jsme znali z výchozí situace a a b a odvodili jsme e. Další kombinací je, že známe a a e. Právě na základě tohoto zadání jsem nakreslil elipsu na obrázku č. 1. Jak? Jednoduše. Nejprve jsem nanesl na hlavní osu vzdálenosti a a e. Pak jsem vzal kružítko, na něm jsem si naměřil vzdálenost a, a tuhle vzdálenost jsem opět pomocí kružítka vynesl z bodů F1 a F2 coby poloměry dvou oblouků. Oblouky se protnuly v bodě B, čímž známe b. Třetí možnost je, že známe vzdálenosti b a e. Tento případ jistě zvládnete už sami.
Odvození rovnice elipsy
Z toho, jak jsme elipsu nakreslili, můžeme elipsu definovat, jako geometrické místo bodů, které mají od dvou pevných a současně různých bodů F1, F2 konstantní součet vzdálenosti 2a, který je větší než vzdálenost F1F2. Dříve než se pustíme do odvození analytické rovnice elipsy, musíme se rozhodnout, jak elipsu posadíme vůči kartézské soustavě souřadnic. V učebnicích je většinou v tzv. osové poloze, kdy počátek souřadnic je ve středu elipsy a osy elipsy jsou v osách soustavy souřadnic. V normální poloze jsou osy elipsy rovnoběžné s osami soustavy souřadnic. V obecné poloze nejsou osy elipsy rovnoběžné s osami souřadnic. Jak jsem si elipsu posadil já, vidíte na obrázku. Je to trochu atypické umístění, které má své výhody i nevýhody, ale proč zase ne.
Odvození je uvedeno na obrázcích č. 2 a č. 3. Při odvození budeme vycházet z označení na obrázku č. 1.
Na obrázku č. 2 v bodě č. 1 jsou rekapitulována fakta, která plynou jak z definice elipsy a nakonec i ze způsobu kreslení elipsy na naší fiktivní zahradě.
Naším prvním dílčím cílem bude spočíst velikosti průvodičů f1 a f2 (jsou vytaženy červenou barvou). Na obrázku č. 1 vedou z ohnisek do bodu C. Mohli jsme klidně zvolit jakýkoliv jiný bod na obvodu elipsy, ale při naší volbě bodu C je názorně vidět význam vzdáleností n, x a y. Jak jsme se k finálním vzorcům pro f1 a f2 dopracovali, mělo by být zřejmé z podrobně uvedeného výpočtu. Výpočet velikosti průvodičů f1 a f2 je podrobně uveden na obrázku č. 2. Pro zajímavost si můžete spočíst součet f1 a f2. Měl by dle definice elipsy být roven 2a.

Na obrázku č. 3 v bodě č. 3 je podrobně uveden závěr výpočtu vedoucí k odvození rovnice elipsy, je označena písmenem c. Za povšimnutí stojí skutečnost, že posun středu elipsy vůči počátku souřadnic o kladnou vzdálenost a se odrazil ve výsledné rovnici. Kdybychom elipsu umístili do osové polohy, místo výrazu (x – a)2 by ve vzorci vystupoval pouze výraz x2.

Pokud vás zajímá problematika transformace souřadnic při zavedení nové souřadnicové soustavy, doporučuji vám přečíst si můj elementární úvod do této problematiky zde. Po jeho přečtení byste bez problému měli umět napsat rovnici elipsy v osové a normální poloze při libovolném umístění středu elipsy vůči počátku souřadnic. Pokud jde o obecnou polohu, tedy když osy elipsy nejsou rovnoběžné s osami souřadnic, jsou vzorce trochu složitější. Pokud vás tahle problematika zajímá, doporučuji si vyhledat vhodnou literaturu.
V bodě č. 4 je odvozen obecný vzorec parametr p, což je polovina délky tětivy procházející ohniskem kolmo k hlavní ose, viz obrázek č. 1. Výpočet je při našem nastavení počátku souřadnic a umístění os x a y je zcela triviální. No, a to je to hlavní pro tentokrát vše. Pro ty, kteří chtějí vědět jak se dopracovat k vzorci pro výpočet obsahu elipsy na zákaldě znalosti obsahu kruhu jsem zařadil malý dovětek.
V Brně 30. srpna 2019.
Výpočet obsahu elipsy
Všeobecně známý výpočet obsahu elipsy jsem již na svých stránkách uvedl, a to zde. Jenomže výpočet je založen na znalosti základních elementů integrálního počtu, což nemusí být pro mnohé čtenáře až tak zábavné čtení. Zkusme si odvodit obsah elipsy pouze se znalostmi matematiky ze základní školy.
Podívejme se na obrázek č. 4. Nad stejným průměrem jsou nakresleny elipsa a kružnice. Nevšímejte si pomocných čár, které jsem použil k nakreslení elipsy (viz oskulační kružnice v předchozím textu). Podívejme se nejprve na přímku ABC. Intuitivně vidíme, že délku AB dostaneme vynásobením délky AC nějakým číslem v rozsahu od 0 do 1. Když přímku ABC posuneme jinam, např. kousek doprava do polohy DyY, souřadnice bodů B a C se změní na y a Y, ale stále vidíme, že délku Dy dostaneme vynásobením délky DY nějakým číslem v rozsahu od 0 do 1. Co když tohle číslo v rozsahu od 0 do 1 je stále stejné bez ohledu na posun přímky ABC? A co když je dokonce spočitatelné z parametrů elipsy?
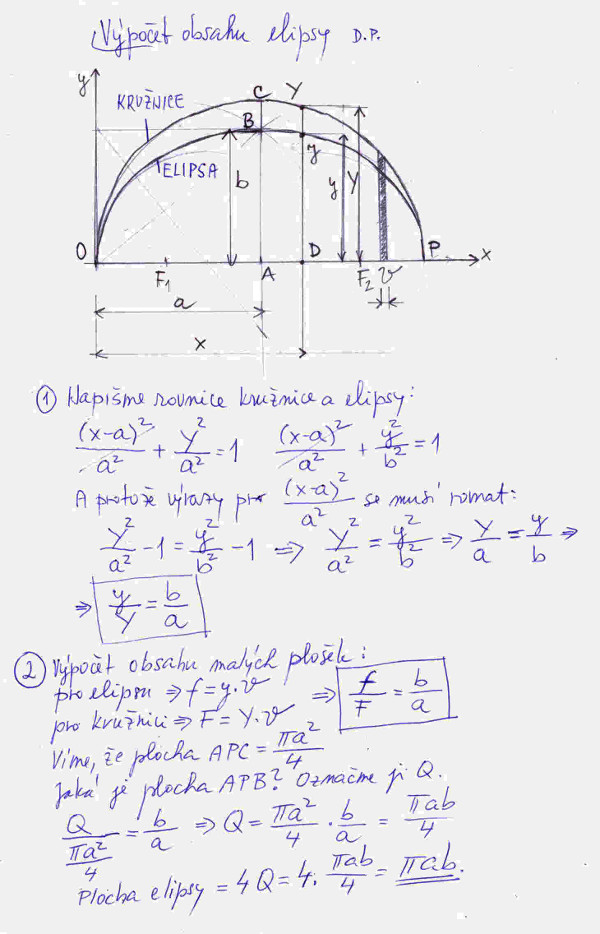
A víte, že je to pravda! V bodě 1 je uveden důkaz téhle skutečnosti. Pro souřadnici x odpovídající souřadnici na ose y značíme pro elipsu opět y a pro kružnici Y. Jednoduše jsme dokázali že poměr y/Y = b/a bez ohledu na polohu přímky DyY. Pokud máte nějaké povědomí o geometrických transformacích tak tahle skutečnost není vůbec náhodná, je důsledkem toho, že v osové afinitě (to je jedna z mnoha geometrických transformací) je obrazem kružnice právě elipsa. Pokud poznámka o transformaci je pro vás trochu těžká, nic se neděje, pro náš výklad je jenom doplňující. A možná, že vás inspiruje k zájmu o geometrické transformace.
Nás ale zajímá obsah elipsy. Opět se podívejme na náš obrázek, na něm je nakreslen malý proužek o šířce théta. Tam si představíme i nové souřadnice y a Y. Navíc když si představíme, že proužek je málem nekonečně úzký, můžeme alespoň přibližně říct, že obsah proužku pro elipsu je y.théta a pro kružnici Y.théta. A ejhle poměr obsahu obou kroužků je opět roven poměru b/a, což je nějaké číslo od 0 do 1. Když to platí pro proužky, proč by to nemělo platit pro obsah jak celé kružnice, tak i elipsy?! To víte, že to platí! V bodě č. 2 je na základě této intuitivní skutečnosti spočten obsah elipsy. Jak prosté!