Transformace souřadnic při zavedení nové souřadnicové soustavy
Dušan Polanský
Nikdy mě ani ve snu nenapadlo tvrdit, že matematika coby maturitní předmět je dobrý nápad. Za dobrý nápad to určitě nepovažuji už jenom proto, že je tu spousta jiných předmětů, co by mohly být stejně dobře povinným maturitním předmětem jako matematika, kupříkladu fyzika, chemie, biologie, informatika. Ovšem v žádném případě si to nemyslím proto, že matematiku nemusím, naopak, docela ji mohu, třebaže maximálně tak na úrovni okresního přeboru, což mi ale stačí. Nakonec kolik inteligence a šikovnosti člověku Bůh nadělí, s tím si musí umět vyjít. Když ne, obvykle to skončí zle nedobře.
S tou povinnou matematikou to máte jako kupříkladu s tělocvikem, každý tělocvikář si myslí, jelikož on to má dáno fyzicky od Hospodina, že každý musí lozit a skákat po stromech jako opice. Pochopitelně tělocvikáři tvrdí, že to není pravda, že oni chtějí jenom děti uměly to a ono a tamto. Jednou u vína mi jedna paní učitelka vyprávěla, jak jsou její žáci neschopní, že jim nejde němčina, přitom, že jim vysvětluje, že je to jako v matematice, že německá věta má pevně danou strukturu. A já jí povídám: Tak to jste jistě dobrá v matematice. Co vám budu povídat, urazila se. Jinak já jsem trochu dobrý v matematice, ale nic moc jazyky. Snad jste pochopili, co chci říct. Ale vraťme se raději k nemilované matematice.
Z matematiky mám rád i jednoduché úvahy, které často v učebnicích chybí, protože autor si buď myslí, že je to samozřejmost, nebo ani neví, že lze problém tak vyložit. Na malou ukázku toho, co mám tím na mysli, jsem napsal tento text.
Většina z nás si možná ještě vzpomene na rovnici kružnici, jejíž střed je v počátku souřadnic. Může vypadat například nějak takto: x2 + y2 = 62. Teď si představme, že chceme střed téhle kružnice umístit do bodu S(–3, 2). Jak bude znít rovnice této kružnice se středem v tomto bodě? Osobně vzoreček, podle něhož se dopracujeme k výsledku neznám, třebaže je uveden v každé knize o analytické geometrii. Já si tuhle věc pamatuji trochu jinak.
Podívejte se na obrázek č. 1 (číslo obrázku zjistíme po najetí myši na obrázek). V bodech č. 1 až č. 4 můžete vidět úvahy, podle kterých vím, kdy se jedná o posun křivky doleva, nebo doprava, potažmo nahoru nebo dolu. V bodě č. 5 je mnemotechnický kříž, jenž je výsledkem předchozích úvah, a ten si občas pamatuji. Kříž nám říká, že když chceme obecnou křivku posunout směrem doprava nebo nahoru musíme použít znaménko mínus, pokud směrem doleva nebo dolu znaménko plus.

Zkusme podle tohoto pravidla posunout již zmíněnou kružnici x2 + y2 = 62 tak, aby její střed ležel v bodě S(–3, 2). Vidíme, že střed kružnice chceme posunout doleva a nahoru, takže rovnice podle naší mnemotechnické pomůcky bude znít (x + 3)2 + (y – 2)2 = 62.
Když už jsme s tím posunem začali, víme, že se nemusí posouvat pouze křivky, ale klidně i celá souřadnicová soustava, tedy její počátek, nakonec i nadpis tohoto textu o tom vypovídá. Je zřejmé, že posun musí být vůči něčemu (bohužel absolutní bod podle fyziků nemáme k dispozici), v našem případě vůči původní souřadnicové soustavě. Tím, že zavedeme novou souřadnicovou soustavu, změní se v nové soustavě i souřadnice bodů, které v původní soustavě měly určité hodnoty. Jenom pro základní informaci si uveďme, že transformace souřadnic při změně souřadnicové soustavy ve velmi obecných prostorech, např. Riemannových, je počtářsky poměrně složitá záležitost. Věci se ještě více komplikují při pohybu nové souřadnicové soustavy vůči původní při požadavku zachování neměnnosti určité veličiny (ve fyzice obvykle rychlost světla). Tady nám ale nepůjde o takové složitosti, my si vyložíme ten nejjednodušší případ, tedy transformaci souřadnic při posunu souřadnicové soustavy v Euklidovském prostoru, tedy nebudeme uvažovat ani otočení, ani pohyb nové souřadnicové soustavy vůči původní. Díky tomuto omezení vystačíme bohatě s látkou ze základní školou. Pokud by vás tahle jednoduchost neuspokojila můžete si přečíst např. moje povídání o transformaci prostorovočasových souřadnic v případě, že nová souřadnicová soustava se vůči původní pohybuje určitou rychlostí ve směru osy x. Název povídání je: Minkowského prostoročas. Ovšem opatrně, v žádném případě se ani zdaleka nejedná o ten nejsložitější případ.
O co nám v našem jednoduchém příkladu jde, je patrné z obrázku č. 2. Máme původní souřadnicovou soustavu P(x,y), my ale z jakýchsi důvodů potřebujeme zavést novou souřadnicovou soustavu N(x´,y´), která je vůči původní souřadnicové soustavě posunuta o určité hodnoty ve směru osy x a osy y, nevylučujeme ani případ, že jedna hodnota posunu nové soustavy je nulová. Teď mějme bod B, jehož souřadnice v původní soustavě jsou B (x,y), pak se ptáme, jaké budou jeho souřadnice B(x´,y´) v nové soustavě. V našem příkladu není problém zjistit nové souřadnice bodu B(x´,y´) pouhým pohledem, viz obrázek, ale my chceme najít obecné pravidlo, pomocí něhož se k novým souřadnicím dopracujeme výpočtem. Ale již není co vymýšlet! Vše potřebné již známe z úvah na obrázku č. 1, akorát teď nebudeme posouvat křivku, ale počátek nové souřadnicové soustavy oproti počátku původní (vztažné) soustavy. Souřadnice bodu v nové souřadnicové soustavě spočteme ze dvou jednoduchých rovnic: x´ = x ± x-ová souřadnice počátku nové souřadnicové soustavy, y´ = y ± y-ová souřadnice počátku nové souřadnicové soustavy. V těchto vzorcích jsou x a y souřadnice bodu v původní (tedy neposunuté) soustavě. Správné znaménko určíme podle našeho mnemotechnického kříže z obrázku č. 1.
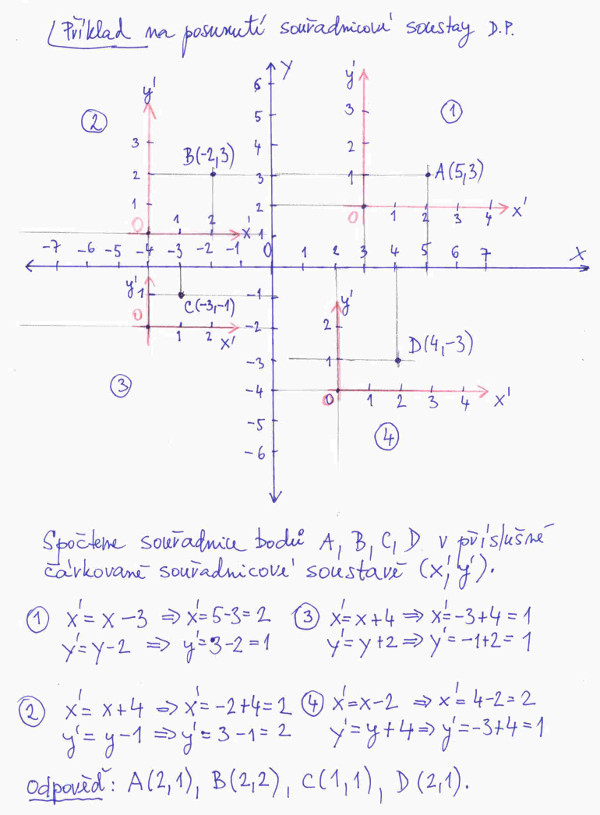
Na obrázku č. 2 můžete vidět dokonce čtyři nové souřadnicové soustavy N(x´,y´) různě posunuté vůči původní vztažné soustavě P(x,y), to proto, abychom si vyzkoušeli všechny možnosti posunu. Dále jsou dány čtyři body A, B, C a D a jejich souřadnice v původní souřadnicové soustavě. Naším úkolem je spočíst souřadnice těchto bodů v příslušné nové souřadnicové soustavě N(x´,y´). Za novou souřadnicovou soustavu pro ten který bod, považujeme tu, která se nachází ve stejném kvadrantu jako bod. Příslušné výpočty jsou rovněž uvedeny na obrázku č. 2. No a to je pro tentokrát vše.
V Brně 7. května 2019.
A pak že holky se nazajímají o matematiku. Středoškolačka se ptá: A co posun na přímce?
Na první pohled je to vcelku jednoduché a jasné, univerzálně platí vzoreček v rámečku na obrázku č. 3. Jenomže hned říct, že to je přece jednoduché a jasné, není až tak jasné. Při důkazu si je potřeba uvědomit, že nový počátek můžeme položit od původního počátku doleva nebo doprava a nějaký libovolný bod, např. K, se může nacházet na 5 pozicích: v původním počátku, v novém počátku, vlevo od obou počátků, vpravo od obou počátků a mezi nimi. Vyzkoušejte si názorně, že vzoreček v rámečku pokrývá opravdu všechny vyjmenované situace. Holt matematika umí být někdy nepříjemně piplavá.
