Objem koule podruhé
Dušan Polanský
Malý úvod
Nedávno mi – asi již starší – čtenář napsal, že by chtěl vědět, co mě vedlo k napsání takové „šílenosti“, jako je můj text o výpočtu objemu n-rozměrné koule (tedy je odkaz na text). Proč? No koukal jsem do několika knih z matematiky v českém a slovenském jazyce, a nikde jsem v té době na výpočet objemu n-rozměrné koule nenarazil, na wikipedii jsem našel jenom výsledný vzorec, a tak jsem ten výpočet na své stránky dal. Tím netvrdím, že podrobný výpočet někde na internetu není.
Koule si jistě zvýšenou pozornost zaslouží. Je to nejkrásnější a geometricky nejdokonalejší těleso v našem reálném světě. Mezi plochami uzavírajícími daný objem má kulová plocha nejmenší obsah a naopak, mezi plochami s daným obsahem uzavírá kulová plocha největší objem. Nakonec matematici, geodeti, astronomové právě kvůli praktické důležitosti koule v přírodě vypracovali celou geometrii zvanou sférická geometrie.
No a abych tu „šílenost“ odčinil k výpočtu objemu koule a jejích částí pomocí integrálního počtu jsem se vrátil, ovšem pouze té naší, třírozměrné. Ovšem pokud jde o množné číslo, tak koule či kule politické, potažmo chlapácké přeněchávám k posouzení politologům, potažmo dámám.
A teď trochu matematiky
Výpočty jsou jednoduché a de facto si vystačíme s jedním vzorcem, což je doklad unikátní symetričnosti koule. Na obrázcích č. 1 a č. 2 je vidět logika výpočtu objemu koule s použitím integrálního počtu; číslo obrázku se objeví po najetí kurzoru myši na obrázek.
Na obrázku č. 1 je vzorec pro výpočet objemu koule při rotaci jednotlivých kružnic kolem osy x.
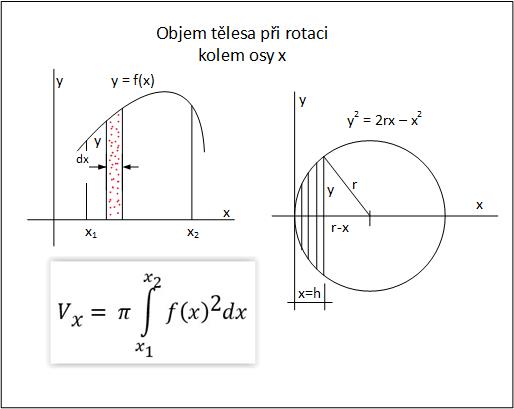
Na obrázku č. 2 je vzorec pro výpočet objemu koule při rotaci jednotlivých kružnic kolem osy y.
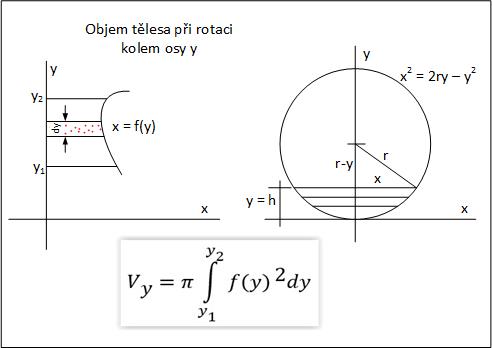
Pokud jde o výpočet objemu kulové úseče, stačí jenom správně nastavit integrační meze, v našem případě se integrační proměnná mění od 0 do h. Příslušné výpočty vidíme na obrázku č. 3.
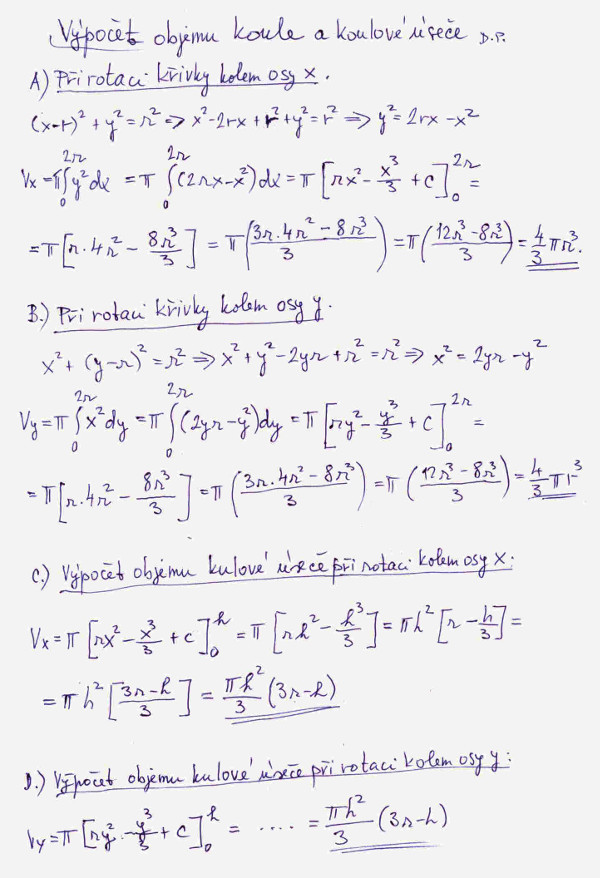
Teď přistoupíme k výpočtu kulové vrstvy, označení veličin je zřejmé z obrázku č. 4.
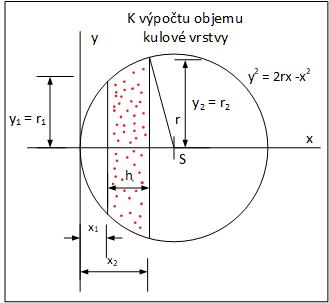
Výpočet objemu kulové vrstvy je sice velmi podobný výpočtu objemu koule, jenom na nás čeká malý algebraický problém. Ve výpočtu vystupují vzdálenosti x1 a x2, ovšem kvůli větší eleganci bychom je chtěli nahradit jejich rozdílem x2 - x1, tedy tloušťkou kulové vrstvy h. Způsobů, jak to udělat bude asi více, ten který jsem použil já, vidíte na obrázku č. 5. Vzoreček pro rozdíl třetích mocnin se až tak často nepoužívá, také já jsem si ho musel vyhledat na internetu. Pak výpočet šel již bez větších problémů.
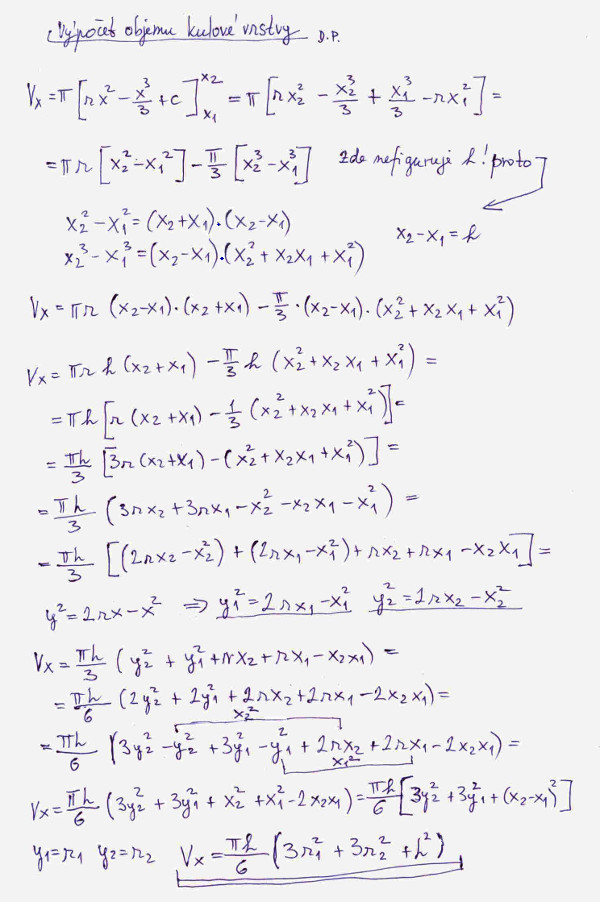
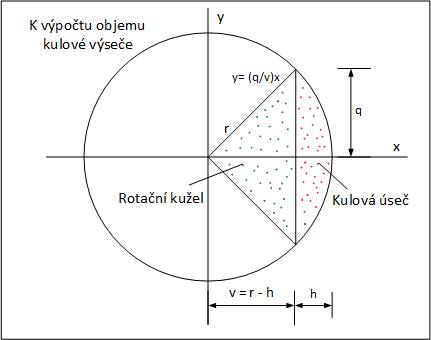
Výpočet objemu kulové výseče se provede tak, že sečteme objem rotačního kužele a kulové úseče. Objem kulové úseče spočíst již umíme. Výpočet rotačního kužele není vůbec složitý, je založen na skutečnosti, že kolem osy x rotuje přímka s počátkem ve středu koule. Stačí znát rovnici této přímky ve tvaru y = kx, kde k je směrnice přímky. A směrnice to je tangens příslušného úhlu. Vzoreček pro výpočet objemu zůstává stejný jako u výpočtu křivky rotující kolem osy x. Označení veličin je zřejmé z obrázku č. 6. Vlastní výpočet je na obrázku č. 7.

No a to by mohlo být vše. Pochopitelně příslušné výsledné vzorce lze nalézt v každé matematické příručce či tabulkách. Nám ale šlo o něco zcela jiného: ukázat eleganci podobných výpočtů integrálním počtem. Holt i matematika je nejednou o eleganci.
V Brně 15. srpna 2023, v den mých 71. narozenin. Ach jo!