Něco málo o těžišti
Dušan Polanský
V nedávno publikovaném textu pod názvem Konkurence je i v matematice – doporučuji si jej pročíst, jelikož s pojmy tam zavedenými a vzorečky tam zmíněnými budu šermovat i zde – jsme si vysvětlili názorně pojem nekonečně malé veličiny, a také jsme si řekli, že moderní matematika tento pojem moc nemusí. Na ukázku použití těchto veličin jsme si spočetli dva příklady z hydrostatiky. Popravdě na tento text jsem žádný ohlas kvůli jeho triviálnosti ani moc nečekal, spíš jsem jej napsal jen tak pro radost, jako když si koupíte nějakou blbůstku v obchodě, ale div se světe nakonec byl, ne sice veliký, ale byl. A byla i prosba, zda bych ještě nějaký vzorový, ne moc těžký, příklad nepřidal. Takže přidávám, a sice bude na výpočet těžiště prachobyčejného pravoúhlého trojúhelníka. Těžiště jsem zvolil proto, že tento pojem se již vysvětluje na základní škole ve fyzice a v geometrii. Takže teď honem zpět do lavic na základce. Popravdě osobně bych se tam nerad vrátil, jelikož v osmičce a devítce mi matematiku málem definitivně zhnusila jedna dáma, která byla přesvědčena, že vyučuje matematiku výborně, což jistě není váš případ.
Těžiště pro fyziky je bod, v němž si můžeme představit soustředěnou veškerou hmotu nějakého tělesa z hlediska fungování zákonů dynamiky; vzpomeňte si na tři zákony Isaaca Newtona z fyziky. I proto se někdy těžišti ve fyzice říká hmotný střed. Tady je názorně vidět, jak účel světí prostředky, a že abstrakce se občas hodí i fyzikům. V geometrii na základní škole se na těžiště jde oklikou, přes těžnici trojúhelníka, což je úsečka, jejíž jedním koncovým bodem je vrchol trojúhelníka a druhým koncovým bodem je střed protější strany. No a pak se sdělí, ale již nedokazuje, že všechny tři těžnice procházejí týmž bodem, který se nazývá těžiště trojúhelníka.
Naše úloha nebude vůbec těžká. Zadání je jednoduché: Máme určit polohu, tedy souřadnice x a y, těžiště pravoúhlého trojúhelníka zobrazeného na obrázku č. 2; číslo obrázku se vám zobrazí po najetí kurzoru myši na obrázek. Všimněme si, že přepona je definována funkcí y = 2x. Dodejme, že trojúhelník je vyroben z velmi tenkého materiálu s konstantní hustotou. A ještě dodám, že příklad jsem úmyslně vymyslel tak, aby nám souřadnice těžiště vyšly hezky v celých číslech.
Úlohu vyřešíme třemi způsoby: geometrickým s využitím pojmu těžnice trojúhelníka, pak po středoškolsku tím, že použijeme něco málo z analytické geometrie, a nakonec, a o to nám právě jde, spočteme polohu těžiště s použitím nekonečně malých veličin, a to dokonce dvěma způsoby. Abychom mohli vůbec začít počítat, musíme si uvést vzorce pro výpočet souřadnic těžiště. Ty jsou uvedeny na obrázku č. 1 postupně pod čísly č. 1 až č. 4.
V bodě č. 1 je vysvětlen pojem těžiště na dětské houpačce, tak jak ji známe z dětských hřišť. Z fyziky víme, že pokud je těleso (u nás je to spíš soustava, protože je to houpačka s dvěma dětmi) v rovnovážné poloze (kláda s dětmi je trvale ve vodorovné poloze, tedy děti se nehoupou), musí být výslednice všech sil působících na těleso nulová a u tělesa otáčivého kolem nehybné osy musí být nulový i moment všech sil působících na těleso. Pokud jde o síly působící v rovnovážné poloze, kromě gravitačních sil na děti působí stejně veliké síly reakce, které mají působiště v trámu. Ovšem houpačka má nehybnou otáčivou osu, a tak jsme museli napsat i momentovou podmínku, a právě z ní jsme vypočetli souřadnici těžiště. Jenom dodejme, že moment síly je definován jako součin síly a ramena, na jehož konci síla působí. Síla je F = m.a, v případě naší houpačky F = m.g, kde g je normální tíhové zrychlení. Ovšem g, jelikož figuruje na obou stranách naší momentové podmínky, se vykrátí, takže v podmínce momentové rovnováhy ani není uvedeno.
V bodě č. 2 jsem tuhle úvahu mechanicky zobecnili na více hmotných bodů na přímce. I v tomto případě těžiště je dáno jednou jedinou souřadnicí. Je to proto, že všechny hmotné body leží na jedné přímce.
V bodě č. 3 jsme naši představu zobecnili pro případ, že jednotlivé hmotné body jsou v prostoru, přičemž poloha každého bodu je dána jeho průvodičem (polohovým vektorem), tedy vektorem vycházejícím z počátku souřadnicového systému a směřujícího do příslušného hmotného bodu. Samotné těžiště je pak také určeno svým průvodičem. V případě skalárního zápisu jsou to pak tři vzorce pro souřadnice těžiště.
V bodě č. 4 jsme pojem těžiště zobecnili na spojitou velice tenkou plochu ležící v rovině s hustotou ró. Jak jsme již uvedli v zadání naší úlohy, budeme hustotu považovat za konstantní, ale klidně by mohla být funkcí polohy, tedy ró = f (x,y). K praktickému výpočtu podle vzorců uvedených v tomto bodě se ještě podrobně vrátíme.

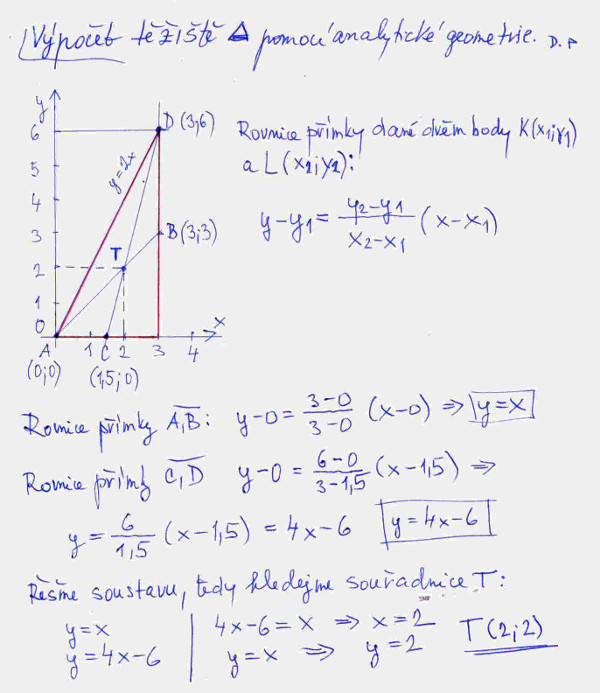
První řešení bude geometrické, tedy s využitím výše zmíněného pojmu těžnice trojúhelníku. Na obrázku jsem zakreslil jenom dvě těžnice, jelikož postačují k určení požadovaných souřadnic. Vidíme, že souřadnice těžiště T jsou T(2; 2). Na stejném obrázku je i druhé řešení, tedy výpočet pomocí analytické geometrie. K výpočtu jsme použili rovnici přímky procházející dvěma body, pochopitelně tahle přímka je v naší úloze těžnice. Opět nám k určení souřadnic těžiště postačují dvě těžnice. Po napsání rovnic těchto přímek, musíme vyřešit soustavu dvou rovnic o dvou neznámých, což nás opravdu nevyčerpá, jelikož soustava je jednoduchá. Opět nám souřadnice těžiště T vyšly T(2; 2).
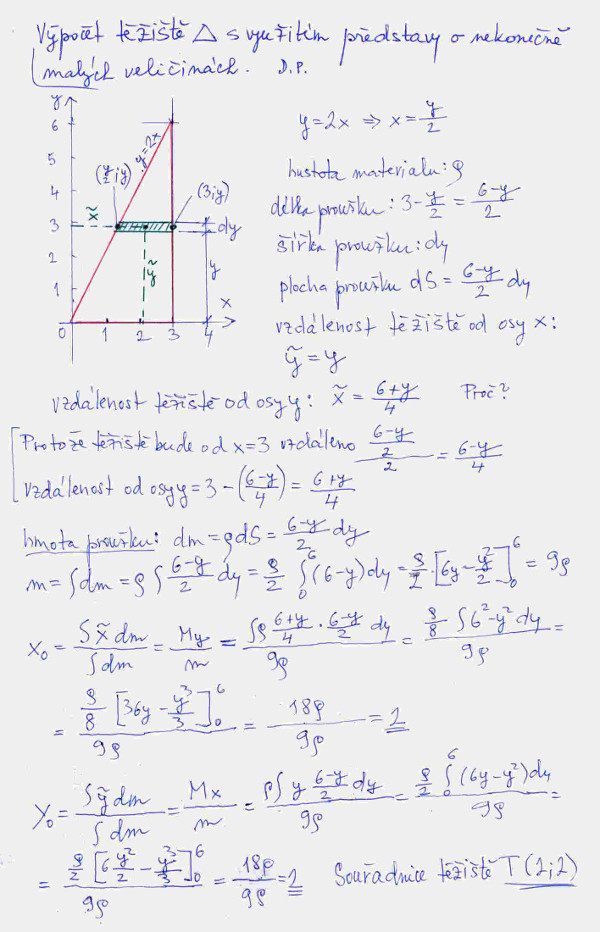
A konečně se dostáváme k postupu výpočtu, kvůli němuž tento text byl napsán. Tedy výpočtu s využitím představy nekonečně malých veličin, v našem příkladu to budou nekonečně malé proužky, jednou svislé a podruhé vodorovné. No a finálně použijeme infinitezimální kalkul, konkrétně integrální počet. Naše představa je velice názorná. Plochu si nejprve rozdělíme na nekonečně malé svislé proužky, viz obr. č. 3. Jeden takový proužek je zakreslen i na obrázku. Těžiště tohoto proužku jsme označili x a y s vlnovkou. Šířka proužku je dx a výška 2x, protože přepona je dána rovnicí y = 2x. Pro náš výpočet je důležité určit souřadnice těžiště jednoho nekonečně malého proužku v závislosti na poloze kroužku, poté plochu dS a hmotnost dm tohoto proužku. Poté již stačí dosadit do vzorců uvedených na obrázku č. 1 pod bodem č. 4. Vlastní výpočet integrálů je pak již triviální.

Podobný postup je aplikován na výpočet při němž uvažujeme nekonečně malé vodorovné proužky, tedy výška proužku bude nekonečně malá veličina dy. Při tomto postupu máme zde dvě malé komplikace: určení délky proužku v závislosti na souřadnici y a určení souřadnic těžiště jednotlivého proužku. Řešení by mělo být zřejmé z obrázku č. 4. Další postup je pak obdobný předchozímu výpočtu. Jak při prvním postupu, tak i při druhém souřadnice těžiště vyšly stejně, tedy T(2; 2), což nás ani nepřekvapilo.
Skromným cílem tohoto populárního povídání bylo ukázat, že nekonečně malé veličiny jsou silným nástrojem při různých výpočtech s využitím infinitezimálního počtu, a že s představou nekonečně malých veličin lze mnohé úlohy řešit velice efektivně při vysoké názornosti celého postupu výpočtu.
V Brně 31. ledna 2022.