O ekvivalenci soustav algebraických rovnic
Dušan Polanský
Po beletristickém povídání o Krásce a Šeredce se patří napsat něco z jiného rangu, např. z matematiky. Protože v životě většina nás bohatě vystačí s kupeckými počty, zvolíme něco lehounkého, jako je např. trubička s našlehanou bílkovou sladkou náplní. Také ji k životu nutně nepotřebujeme, ale občas chuť na ni dostaneme.
Ti starší si ještě možná vzpomenou na Základní devítiletou školu, kde jsme v posledním, devátém, ročníku řešili dokonce soustavu dvou lineárních rovnic o dvou neznámých. Paní učitelka (ta naše mi byla krajně nesympatická) nám přitom kladla na srdce, abychom si správnost výsledku zkontrolovali dosazením vypočtených hodnot proměnných x a y do obou původních rovnic. Když se levé strany rovnic budou rovnat pravým, teprve pak je řešení správné. Pročpak asi na tom trvala?
Než si vysvětlíme proč, zopakujeme si – zatím jenom slovně – postup řešení soustavy dvou rovnic. Když se nebude někdo chytat, nic se neděje, vše si ukážeme později na příkladu. Rovnice jsme obvykle řešili tak, že jsme nějakým šikovným číslem jednu rovnici vynásobili, a pak ji sečetli s druhou rovnicí. Číslo muselo být zvoleno proto šikovně, abychom se zbavili v jedné z rovnic jedné proměnné, čímž v této rovnici vystupovala již jenom jedna neznámá. Vypočíst ji obvykle již nebyl problém. Hodnotu proměnné pak stačilo dosadit do rovnice, kde stále figurovaly obě proměnné, tím se i z této rovnice stala rovnice o jedné neznámé. Spočíst druhou neznámou tím již také nebyl problém.
Jenom si upřesnime, že na základní škole jsme řešili soustavu dvou lineárních rovnic o dvou neznámých, obecně to ale mohou být rovnice obecnější, takzvané algebraické rovnice. To jsou rovnice, kde koeficienty jsou obecně reálná čísla a známé a neznámé veličiny jsou vzájemně vázány pouze algebraickými operacemi: sčítáním, odčítáním, násobením, dělením a umocňováním. Jenom pro úplnost si uveďme, že nealgebraické rovnice obsahují neznámou v transcendentní funkci, např. takovými rovnicemi jsou exponenciální, logaritmické, goniometrické rovnice. Ty se obvykle řeší až na střední škole.
Proč jsme tedy museli ještě dělat zmíněnou kontrolu správnosti řešení? Háček je v tom, že při onom zbavování se některé proměnné, jsme klidně mohli nechtěně provést nesprávnou operaci a přijít o správné řešení. Abychom pointu nesprávné operace pochopili, podíváme se na první obrázek. V něm je vysvětlena ekvivalence dvou soustav rovnic, první soustava je označena číslem 1 v kroužku a druhá číslem 2, opět je v kroužku. Rovnice f2(x,y) je zde vynásobena obecným polynomem, v praxi obvykle vystačíme vynásobením racionálním číslem. O kousek níže je uveden jednoduchý důkaz tohoto tvrzení.

Pod textem „Ale bacha!“ je důkaz, že soustava 3 v kroužku není ekvivalentní soustavě 1 v kroužku. No a právě občas takovou chybu nechtěně uděláme, že soustavu 1 převedeme na neekvivalentní soustavu 3, tj. že libovolným polynomem nebo jenom racionálním číslem vynásobí rovnici f1(x,y), místo správného vynásobení rovnice f2(x,y) (v našem číslování rovnic). Pak se může stát, že takto vzniklá soustava má i řešení, které nevyhovuje původní soustavě.
Ukážeme si to na na soustavě 3x - 4y - 7 = 0, 2x - y - 3 = 0. Již na první pohled soustavě vyhovuje řešení x = 1, y = -1. Vytvořme z ní soustavu: (3x - 4y - 7)*x + 2x - y - 3 = 0 2x - y - 3 = 0. Vznikla z původní soustavy vynásobením f1(x,y) (v našem číslování rovnic) proměnnou x. Po jednoduchém výpočtu zjistíme, že upravená soustava má oproti původní soustavě rovnic navíc řešení x = 0, y = -3. To ale původní soustavě nevyhovuje, tedy se jedná o neekvivalentní soustavy rovnic.
Teorii máme za sebou, teď by správně měla následovat vysvětlení metodiky správného postupu, no a nakonec přijde ukázka řešení podle této metodiky na konkrétním příkladu.
Celá metodika spočívá v tom, že si musíme dobře zafixovat, že rovnici, kterou v určitém kroku řešení násobíme šikovným číslem (obecně polynomem) a přičteme ji k jiné rovnici, musíme nechat v tomto kroku řešení nezměněnou. Doporučuji z vlastní praxe – která je de facto nulová, jelikož používám celý život jenom již zmíněné kupecké počty – rovnici, kterou násobíte šikovným číslem si v příslušném kroku opsat a změnit pouze tu rovnici, k níž rovnici násobenou číslem připočítáme. Číslo, kterým násobíme, a řádek, k němuž naši rovnici připočteme, si napíšeme vedle rovnice vpravo. Pokud má naše soustava více rovnic, ostatní rovnice zůstanou v daném kroku nezměněné. Jsou mistři, co v jednom větším kroku zvládnou více takových kroků, ale my nebudeme divočit. Také proč?
A konečně slíbený příklad. Abychom se odpoutali od základní školy, vybral jsem příklad na řešení soustavy třech lineárních rovnic, je uvedena na druhém obrázku pod číslem 1 v kroužku. Příklad k procvičení je z knihy: Leonard I. Holder: A Primer for Calculus, 2nd Edition, Wadsworth Publishing Company, Belmont, California, 1981. Na konci knihy je uveden výsledek, ovšem není správné mu automaticky věřit, opět nejlépe si výsledek ověřit vlastní kontrolou. Když už jsem zmínil jednu knihu, bylo by hříchem nezmínit vynikající titul: Štefan Schwarz: Základy náuky o riešení rovníc, Vydavateľstvo SAV, Bratislava, 1968. V této knize je i výše uvedený důkaz.
Postup řešení by měl být jasný z obrázku. Nejdříve jsme se zbavili výše popsanou technikou proměnné x, čímž jsme se dopracovali k soustavě dvou rovnic o dvou neznámých, y a z, viz soustavu označenou 2 v kroužku. Proměnnou z jsme vypočetli dosazovací metodou. Jak, to je snad zřejmé. Pak jsme stejnou metodou vypočetli proměnnou y a nakonec x.
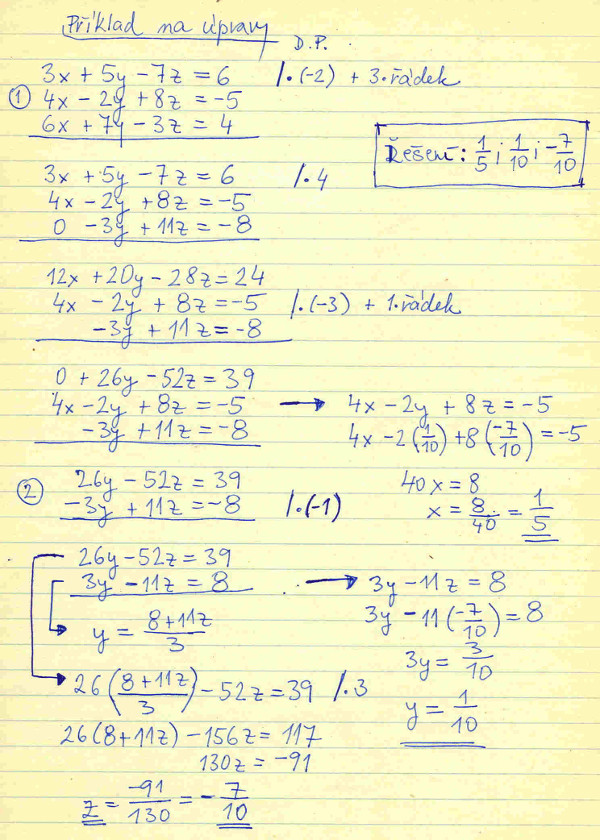
Jinak zmíněná technika zbavování se proměnných vycházející z ekvivalence soustavy dvou rovnic se používá nejen při řešení soustavy rovnic, ale pokud budete studovat na vysoké škole, kde se ještě matematika zatím vyučuje, jelikož prý takových škol ubývá, narazíte na ni při výpočtu determinantů a v maticovém počtu.
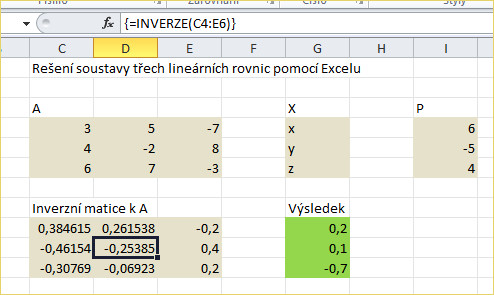
Dodatek pro excelisty: Zmíněná soustava se dá řešit i jinými postupy, kupříkladu pomocí determinantů nebo můžeme k řešení využít Excel. Protože znalost determinantů nepředpokládáme, zkusme naši soustavu vyřešit pomocí Excelu. Zápis soustavy i výsledek je na třetím obrázku. Při výpočtu budeme využívat maticové vzorce, ne každý tuhle techniku zná, tak postup řešení si uvedeme raději podrobně.
Naši soustavu si napíšeme formálně jako rovnici A * X = P. A je matice koeficientů soustavy rovnic, X je vektor neznámých, tedy x, y, z a P je vektor koeficientů pravé strany. Znaménko * označuje maticové násobení, naštěstí nás nemusí jeho definice trápit, jelikož Excel tohle násobení zvládne za nás. Vlastní řešení se napíše maticově takto: X = A-1 * P, kde A-1 je inverzní matice. Opět nás její definice, ani její výpočet z matice A nemusí trápit, protože Excel spočíst inverzní matici umí.
Teď již vlastní postup step by step.
- Spustíme si Excel, je jedno jaký, umí to všecky a přepněme se do prázdného listu.
- Napíšeme si hodnoty A, X, P, nějak tak, jak vidíte na obrázku. Umístění v listu není důležité. Rovněž nadpisy jsou zde jenom kvůli přehlednosti.
- Označíme si oblast, kde Excel vloží prvky inverzní matice A-1, musí mít stejnou velikost, v matematické terminologii rozměr, jako matice A.
- Vyvoláme matematickou funkci INVERZE, dialogové okno požaduje od nás zadat pole (oblast), kde se matice A nachází, myší označíme pole hodnot matice A, na našem obrázku je to oblast C4:E6, a vše potvrdíme OK. Vidíme, že v oblasti pro inverzní matici je zatím jenom jedno číslo v levém horním rohu, jako kdyby Excel zapomněl spočíst i ostatní hodnoty inverzní matice. Aby to udělal, musíme mu sdělit, že takové něco od něho požadujeme. Přesuneme se kurzorem do pole, kde se zadávají vzorce, umístíme kurzor kamkoliv dovnitř textu vzorce =INVERZE(C4:E6) a stiskneme najednou Ctrl + Shift + Enter. A hle, Excel nám spočetl i zbývající hodnoty inverzní matice. Ovšem stále musíme mít při onom složitém stisku oblast, do níž chceme uložit výslednou inverzní matici, označenou! Všimněme si, že do vzorce se na začátek a na konec doplnily složené závorky, nějak takto {=INVERZE(C4:E6)}, takový zápis nám sděluje, že se jedná o maticový vzorec.
- Další krokem bude výpočet maticového součinu A-1 * P. Excel pochopitelně maticové násobení umí. Prvně si označíme oblast, do níž budeme chtít uložit výsledek, na obrázku je to oblast G9:G11.
- Vyvoláme matematickou funkci SOUČIN.MATIC. Vidíme, že dialogové okno má dvě pole. Do jednoho zadáme myší oblast inverzní matice, do druhého oblast P, a vše potvrdíme OK.
- Situace se nám opakuje, výsledná hodnota je jenom v jedné buňce, ale již víme, jak se dopracovat k tomu, aby výsledek byl i v dalších dvou buňkách, tedy tam, kde očekáme výsledné hodnoty proměnných y a z. Přesuneme kurzor kamkoliv do textu vzorce =SOUČIN.MATIC(C9:E11;I4:I6) a stiskneme opět najednou Ctrl + Shift + Enter. A hle Excel nám dopočetl i zbývající hodnoty. Ovšem opět při onom složitém stisku musíme mít oblast, do níž chceme umístit výsledné řešení, označenou! Všimněte si, že do vzorce na začátek a na konec se opět doplnily automaticky složené závorky, což nám sděluje, že se opět jedná o maticový vzorec.
Výsledek je v souladu s naším výpočtem výše, akorát v Excelu jsou výsledné hodnoty zapsané jako desetinná čísla, kdežto při ručním výpočtu jsme je zapsali ve formě zlomků. A to je vše.
V Brně 8. května 2015.