Něco málo o lineární perspektivě I
Dušan Polanský
V té chvíli byla celá plocha zakryta železnou oponou, nakvap pomazanou křiklavými krajinami a nemotornou perspektivou.
Citace z Maurice Leblanc: Tři oči. Autorizovaný překlad (z francouzštiny) Arnošta Bareše, Československé podniky tiskařské a vydavatelské, Praha, 1922.
Prolog
Nevím, jak znáte či neznáte Brno, ale ulice Pekařská a Kopečná jsou propojeny fragmentem ulice Leitnerovy. V této ulice jsem kdysi dávno docela rád a často chodíval do vinotéky, jenomže ta již několik let jednoduše není, ale naštěstí teď nám nejde o víno. Zmíněný fragment totiž tvoří většinou schody stoupající ve směru k Pekařské. No a jednou, jak jsem vypadl ze zmíněné vinotéky, a vydal se směrem k Pekařské, všimnul jsem si staršího pána, jak stal kousek pod zmíněným schodištěm a skicoval si obyčejnou tužkou do bloku ony schody s jejich okolím. Nedalo mi to, a po očku jsem mu mrknul do bloku, načež pán se zatvářil kysele. Já na to: „Jen jsem se chtěl podívat, zda se vám schody sbíhají do jednoho úběžníku nebo do dvou úběžníků. Zatvářil se ještě kyseleji a opáčil: „Co vám do toho, nakreslete si je sám, jak mi tu radíte, a vůbec, nemám žádné umělecké školy, jsem samouk, kreslím, že mě to baví a jak to umím.“ A tím setkání s kreslířem či malířem skončilo.

A ještě jedno pomyslné setkání s malířem. Když se podíváme na kresbu na umělecké pohlednici vlevo, hned vidíme, že tohle musel nakreslit malíř velice dobře znalý zásad lineární peperspektivy a kresby stínu. Nelze se ani divit, autorem je vynikající malíř, grafik a především architekt Alfréd Piffl (1907 - 1972). Pokud chcete o něm vědět více, stačít si zadat jeho jméno do vyhledávače. Opětovně žasnu nad !zdánlivou! lehkostí, s jakou tahle kresba byla vytvořena. Ovšem zkušeně oko okamžitě vytuší za onou pomyslnou lehkostí kresby značné teoretické znalosti a praktické dovednoti tvůrce.
Po setkání s malířem na Leitnerce jsem si řekl, že bych mohl napsat něco zcela elementárního o lineární perspektivě, tam se totiž každá linie sbíhá do úběžníku, a dát to na svůj web a případně i nějaké ty schody v perspektivě nakreslit. Jenomže nějak ne a ne. Až na jaře letošního roku v době pandemie koronaviru jsem se snažil vnučce (to byla v třetí třídě základky) vysvětlit, že domeček se má správně kreslit jinak, než ho děti běžně kreslí, jelikož tak ho doopravdy nevidíme. Ukázal jsem jí asi jak, ale malé děti mají problémy s prostorovým viděním, takže moje snažení se nedočkalo vyslyšení. Snad později. Ovšem jeden plus to mělo, sice opožděně, ale teď v září jsem se povídání o perspektivě rozhodl konečně dát na papír, přesněji na web.
A hned si zajistím i alibi. Můj text není v žádném případě kurzem lineární perspektivy (jsem jenom amatér, který o tom něco málo ví), je to jenom povídání, které má dát čtenáři elementární vhled do teorie perspektivního zobrazování a hlavně jej inspirovat k dalšímu studiu a především k vlastní tvorbě. Kurz má tři díly. První díl bude věnován tomu nejelementárnějšímu, ale asi také nejdůležitějšímu objektu, a to perspektivnímu zobrazení krychle. Krychlí to totiž v perspektivě vše začíná a někdy i končí. Druhý díl bude věnován kreslení schodů a třetí stínů. Na konci třetího dílu mého povídání je uveden seznam literatury (z mé knihovny, určitě jsou i další tituly, kupříkladu přímo k stažení z internetu), v níž se o lineární perspektivě dozvíte další podrobnosti. K jednotlivým titulům jsem připojil i krátký (já) komentář.
A ještě poznámka: Text je určen pro začátečníky. Důsledně se vyhýbám přesným popisům, tak typickým pro deskriptivní geometrii, jelikož tyhle nejednou začátečníka spíš vystraží, než aby jej vedly k dalšímu studiu.
Uff, to byl ale dlouhý a málem zbytečný prolog, takže raději už začneme.
Pointa
Úvodem je asi vhodné připomenout, že způsobů zobrazování je habaděj. V praxi se daleko nejvíce používá ortogonální zobrazování, při němž obvykle pracujeme s půdorysem, nárysem a bokorysem, přičemž pohled na příslušnou stranu objektu je vždy kolmý. Pokud to nestačí, a je potřeba zachytit i vnitřní uspořádání zobrazovaného objektu, tak se již zmíněné pohledy doplní podélným či svislým řezem objektu. Axonometrické zobrazování je pro lidské oko názornější. Při něm jsou vidět dvě boční stěny objektu a jeho vrchní plocha, je to tedy nadhled. U lineární perspektivy nám jde o dosažení maximální podobnosti se skutečným pohledem lidských očí na zobrazovaný objekt potažmo objekty. Stručně asi tak: zobraz realitu tak, jak ji vidíš z místa svého stanoviště svýma očima. V reálném životě se obvykle pohybujeme, čímž měníme své stanoviště, také je rozdíl, zda stojíme či sedíme, nebo se na objekt díváme shora, zdola, zboku apod. Také je důležitá šíře (úhel) našeho pohledu, která je výrazně omezena vlastnostmi našeho oka. A právě kvůli této variabilitě parametrů, které ovlivňují kvalitu zobrazení objektů při lineární perspektivě je tohle zobrazení náročnější na pochopení. Ovšem odměna v podobě hezkých realistických zobrazení je obvykle příjemně sladká.
Perspektivně vidíme stále, ovšem ne vždy je efekt výrazně stejný. Kupříkladu když jedeme autem a díváme se před sebe, tak linie přímé vozovky se před námi v dáli sbíhá do pomyslného bodu zvaného úběžník. Ještě markantnější to lze pozorovat, když se postavíme na kolejový svršek mezi koleje na rovném úseku a díváme se do dálky, koleje se nám opět sbíhají v úběžníku. Podobně když dlouhý vlak vidíme ujíždět kamsi do dáli, vidíme, že lokomotiva je nejmenší a poslední vagón největší. Obdobný jev sledujeme i v dlouhé rovné ulici nebo aleji, rovnoběžné linie domů nebo korun stromů se rovněž sbíhají do pomyslného úběžníku. Ale i v bytě, když se postavíme do jednoho rohu pokoje, vidíme, že nábytek a prostor se rovněž sbíhá pomyslného úběžníku. Níže můžete vidět pohlednici s architektonickým návrhem sokolovny, přičemž návrh důsledně respektuje principy lineární perspektivy. V lineární perspektivě je důležité, že se díváme očima a všechny promítací přímky (paprsky) směřuji z našich očí směrem k zobrazovanému objektu. Ale protože naše oči jsou vzhledem k zobrazovaným objektům od sebe minimálně vzdáleny jednoduše mluvíme o oku, dokonce se doporučuje, abychom se při použití perspektivy dívali pouze okem jedním, čistě teoreticky ano, ale v praxi tak i onak.

Nechť je tedy naše oko středem promítání, což implikuje, že perspektiva patří do středového (centrálního) promítání. Dodejme, že v deskriptivní geometrii se obvykle více pozornosti věnuje rovnoběžnému promítání. Jinak perspektiv je hodně, např. cylindrická, sférická, křivočará, divadelní, reliéfní, ale my si budeme povídat o lineární, při níž chceme objekty zobrazovat tak, jak objekty či protor opravdu vidíme. Ovšem malé upozornění tzv. vojenská perspektiva je jedním z typů axonometrického zobrazování, tedy není perspektivou, o které si zde budeme povídat. Zajímavá je kreslířská perspektiva, to je taková, kde přidáme do lineární perspektivy i barvy a stíny, aby obraz vypadal jako živý, ovšem přitom kreslíř či malíř musí důsledně ctít realitu. Pochopitelně barvu a stíny lze přidat do kterékoliv z perspektiv.
Ono vůbec je rozdíl, když kreslí např. stavař projektant či architekt, anebo výtvarník. Architekt musí důsledně dodržovat pravidla perspektivy a ctít realitu, potažmo návrh příští reality, výtvarníci mají daleko více volnosti, holt jsou to umělci. Proto si také všimněte, že hlavně malíři bez uměleckého vzdělání občas nectí zásady perspektivy. Ovšem není to jenom o sbíhání přímek do úběžníků. Na pohlednici Hlavního nádraží v Hradci Králové je hezky vidět, jak perspektivně se mění i šíře a výše oken. O perspektivním členění plochy si více povíme v třetím díle našeho seriálu.

Takže teď už víme, že lineární perspektiva patří k středovému promítání. To je dáno středem promítání S a průmětnou, na kterou promítáme objekty za průmětnou. Teoreticky mohou být objekty i před průmětnou, ale v praxi se tento způsob využívá výjimečně. Pro středový průmět A´ bodu A (ten je kdesi za průmětnou) platí, že je dán průnikem promítací přímky vedené z bodu S do bodu A s průmětnou. Průmětně budeme dále říkat raději zobrazovací rovina, jelikož průmětna je cítit deskriptivní geometrii, a ta se již moc na dnešních školách nepěstuje.
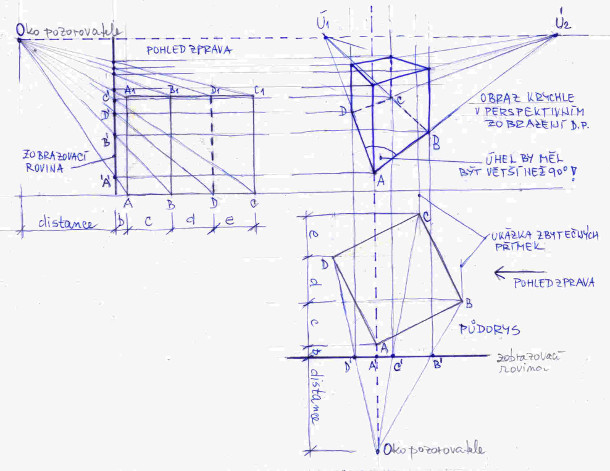
Jako u všeho odborného či neodborného i lineární perspektiva má své názvosloví. Na obrázku č. 1, číslo obrázku zjistíte po najetí kurzoru myši na obrázek, je zakresleno typické názvosloví lineární perspektivy, ovšem nedivte se, když v literatuře narazíte i přesto na mírné názvoslovné odchylky. Výška oko se pohybuje kolem 165 cm. Distance musí být taková, aby zobrazované objekty nebyly příliš zkreslené, ono slovíčko lineární právě říká, že objekty nejsou zkreslené, že je vidíme víceméně jako naše oko. Distance by měla být větší než 20 cm a objekt by měl ležet v zorném kuželi, což je rotační kužel o vrcholu v oku O, s osou OH, s odchylkou alfa od osy OH a s podstavou v zobrazovací rovině. Úhel alfa by měl být maximálně 30 °. Když označíme poloměr podstavy zorného kužele na zobrazovací rovině r, tak perspektiva objektu (tedy to, co nakreslíme), musí ležet uvnitř zorné kružnice k = (H, r). Jinak distance by měla být maximálně 3r. Naplnění těchto požadavků by nám mělo zajistit, že zobrazované objekty budou odpovídat nezkreslené realitě. Mezi námi, zkušený kreslíř ví, kam se postavit a jak se na zobrazovanou realitu podívat, tedy vybrat správnou výšku horizontu a osu pohledu (přímka OH). Prostě jako vše, chce to cvik neboli cvik dělá mistra.
Shrňme si zatím řečené. Lineární perspektiva je dána: hlavním bodem, horizontem, distancí a výškou oka, přičemž hlavní bod leží na horizontu.

Teď se ještě vrátíme k obrázku č. 1. Je dobré vědět, že výška horizontu se mění podle polohy oka, tedy zda stojíme nebo sedíme. Ti, co byli u moře to znají velice názorně, jelikož horizont je linie na rozhraní moře a oblohy. Na obrázku je zakreslen perspektivní obraz čtverce, který leží na základní rovině, tedy na rovině (zemi), kde stojí kreslíř. Všimněte si nejdůležitějšího poznatku: perspektivní průměty rovnoběžných přímek 1,2 a 3,4 kolmých na zobrazovací rovinu se sbíhají do bodu H, což je současně v našem příkladu i úběžník. Jinak přímkám kolmým na zobrazovací rovinu říkáme hloubkové přímky. Pokud se podíváme na perspektivní obrazy úseček 2,3 a 1,4 rovnoběžných se zobrazovanou rovinou vidíme, že čím je přímka více vzdálená od zobrazovací roviny, tím je její obraz kratší, pouze přímka 1,4 si zachovává svoji velikost, to proto, že leží v promítací rovině, což platí pro všechny přímky, které leží v zobrazované rovině. Dále vidíme, že rovnoběžnost těchto přímek se zachovává. Jinak ještě platí další vlastnosti perspektivy, ale o tom více v doporučené literatuře.
Na obrázku č. 2 vidíte, jak vzniká perspektivní obraz krychle z jejího půdorysu a bokorysu. I v tomto obrázku je úběžník Ú totožný s bodem H, což je ale jenom speciální případ, obecně tomu tak není. Je to proto, že jedna stěna krychle je rovnoběžná se zobrazovací rovinou a osa pohledu jde přesně středem krychle. Popravdě zkušený kreslíš si nikdy osu pohledu takto nevybere už jenom proto, že nejsou vůbec vidět bočné stěny.

Na dalším obrázku, tedy č. 3, tomu již tak není. Osa pohledu sleduje svislou hranu A a navíc krychle je vůči zobrazovací rovině natočena a hle vidíme, že úběžnice se nám sbíhají do dvou úběžníků a vidíme i dvě bočně stěny. Ovšem perspektivní obraz má jednu vadu, když se podíváte na krychli v perspektivě, speciálně na úhel sevřený stěnami AD a AB, tak je menší než 90 °, což by nemělo být, prostě to není ono, krychle působí trochu divně. Jak na to, aby se nám to nedělo, si ukážeme v druhém pokračování. Začátečníci občas také přidávají do obrázku zbytečné přímky, viz obrázek. Svislice či horizontály mají být vedeny pouze z bodů na zobrazovací rovině.
V praxi se s krychlí takhle složitě netrápíme. Již jsou vyzkoušené postupy, jak si krychle v různých polohách nakreslit bez větší námahy. Na obrázku č. 4 vidíme tzv. krychlovou síť, tuhle jsem nakreslil podle [2], jejíž základ tvoří zobrazení krychle uprostřed. Jedině, co musíte zvládnout je odhad délky boční stěny, pokud to zvládnete dobře, zadní stěna krychle vám musí vyjít čtverec.

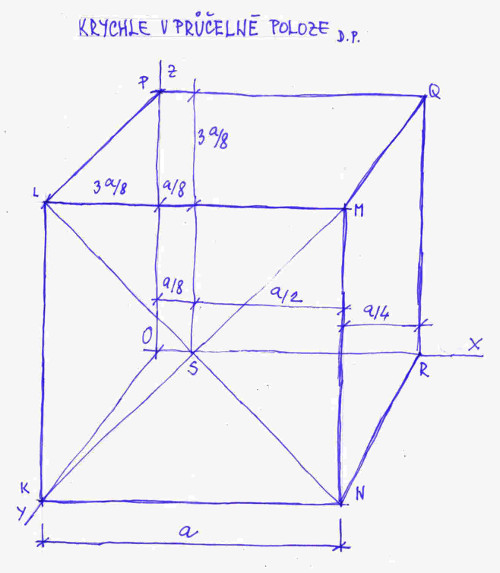
Do podobných či jiných krychlí se pak zakreslují různé objekty, ovšem s tím, že na papír o velikosti např. A4 si nakreslíme pouze jednu krychli. Obvykle se k tomu využívají mechanické postupy. Na průmyslovce jsme většinou používali postup uvedený na obrázku č. 4a, jenž je převzat z literatury [1], kde jsou uvedeny i další postupy. Nejprve si nakreslíme čtverec KLMN o straně a (já jsem zvolil a = 10 cm), pak osu x, na níž naneseme od hrany MN vzdálenost a/4, čímž dostaneme bod R. Na osu x vlevo od bodu S naneseme vzdálenost a/8, čímž dostaneme bod O. Nakreslíme osy y a z. Na osu z naneseme dle obrázku vzdálenost 3*a/8, čímž dostaneme bod P. Nakreslíme zbývající hrany. Zadní stranu tvoří čtverec OPQR. Jednoduše se pracuje s a = 12 cm, jelikož pak vychází a/4 = 3 cm, a/8 = 1,5 cm a 3*a/8 = 4,5 cm.
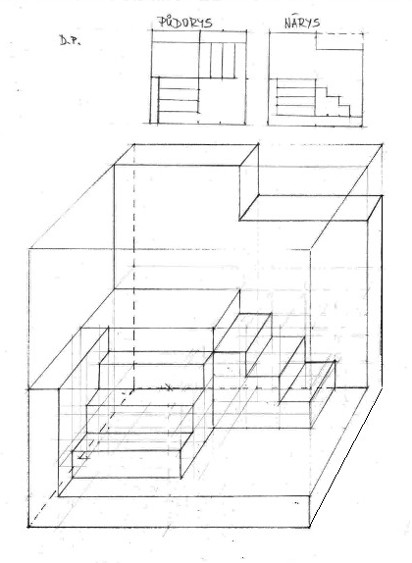
Na konci knihy [1] jsou příklady k procvičení prostorové představivosti. Jsou zde uvedeny půdorysy a nárysy (případně bokorysy) objektů, které máte zakreslit do podobné či jiné krychle. Jako ukázku toho, co se tím myslí, jsem do výše uvedené krychle nakreslil prostorový objekt ze zadání půdorysu a bokorysu. Ovšem např. tohle zadání patří k těm jednoduším.

Tohle zasa k těm složitějším. Ale v [1] jsou i opravdové špeky.
Jak občas s úsměvem říkal na střední škole náš pán profesor Cibulka, autor knihy [1], úběžníků není nikdy dost. Na obrázku č. 5 vidíte nakreslený domeček se sedlovou střechou v lineární perspektivě s využitím čtyřech úběžníků. Tak nějak jsem ho nakreslil i vnučce, ale jak jsem již uvedl, moc jsem nepochodil. A protože cvik dělá mistra, což pán profesor zdůrazdňoval, zkuste si domeček nakreslit při různé výšce horizontu.

Obrázek č. 6 působí složitě, ale je jenom jako složitý. Všimněte si, že hrana krychle v bodě A se dotýká zobrazovací roviny, což je výhodné v tom, že délka této hrany se v perspektivním zobrazení nemění, což je názorně vidět na obrázku č. 1. Právě proto se nakreslení krychle velice zjednoduší. Stačí z půdorysu přenést do spodního obrazce pozice úběžníků a výšku hrany v bodě A, a pak již jenom spojovat linie krychle s úběžníky. Pokud jde o pozice úběžníků v půdorysu jsou nakresleny jako průsečíky rovnoběžek s příslušnými hranami půdorysu krychle s půdorysem zobrazovací roviny. Tohle zjednodušení si můžeme dovolit proto, že krychle je v tzv. nárožní poloze. Jinak tuhle techniku s oblibou využívají při kreslení architekti. Jednu hranu stavby si zvolí šikovně tak, aby se právě dotýkala zobrazovací roviny.

No a poslední obrázek, tedy č. 7. je spíš upozorňovací. Říká nám, že v jednoúběžníkové perspektivě by hlavní bod H a úběžník Ú neměli být od sebe příliš daleko, jelikož pak hrozí veliké zkreslení, což bychom si v lineární perspektivě dovolit neměli. Nakonec si to sami vyzkoušejte, posuňte Ú ještě více doprava. Dolní část obrázku nás zase upozorňuje na skutečnost, že si je potřeba pohlídat vyznačený úhel, měl by být větší než uhel pravý. Pokud tomu tak není, opět hrozí zkreslení, viz také obrázek č. 3. Ale jak jsem již napsal výše, v dalším pokračování si vysvětlíme, jak si s tímto úhlem poradit.

A to je pro první díl vše. V dalším dílu si nakreslíme nějaké ty schody.
V Brně 29. září 2020.
Zde je odkaz na druhý díl seriálu.
Zde je odkaz na třetí díl seriálu.
Příloha č. 1. Pohlednice, které jsou dokladem perspektivního vidění reality naším okem.

Evangelický cirkevní dom v Liptovském Mikuláši.

Ostrava: Dům umění.

Gen. ředitelství Sev. dráhy Ferdinandovy a německé pojišťovny.

Náchod: návrh sokolovny.

Gottwaldov (dnes Zlín): Revoluční třída.

Liberec: sídliště Králův Háj.

Kladno: Rozdělov.

Jaroslav Šetelík: Bratislava.

Jaroslav Šetelík: Kutná Hora.