Něco málo o lineární perspektivě II
Dušan Polanský
V tomto, druhém, díle našeho společného povídání o lineární perspektivě se naučíme kreslit schody, ale ne schody do světlé budoucnosti, ale jenom obyčejné schody, tak je známe z reality, ovšem tak, aby pohled na ně lahodil našemu oku.
Na tomhle obrázku jsou Bystrcké schody při pohledu shora, mají 78 schodů a 4 podesty, ta spodní při tomto pohledu není vidět. Jinak Bystrc je městská část Brna u Brněnské přehrady.
A stejné schody při pohledu zdola. Volně pohozená nákupní taška vlevo je prosím pěkně moje.
Sice tak dlouhatánské schody kreslit raději nebudeme, ale abychom zvládli nakreslit alespoň nějaké, musíme se nejprve naučit rozdělit plochu na opakující se stejné úseky, jelikož pro schody je typická právě repetičnost. Není to nic těžkého, jak můžeme vidět na obrázku č. 8. Zde jsou rozděleny na stejné svislé a vodorovné díly dvě stěny pomyslného objektu. Z bodu PM (tzv. měřicí bod) vedeme přímky do pravého a levého dolního bodu (rohu) ploch, které chceme rozdělit na úseky a a b. Průsečík těchto přímek s přímkou ML (tzv. měřicí přímka) nám vymezí dva úseky, uvnitř kterých vyměříme potřebná rozdělení. Další postup je zřejmý z obrázku. Pokud jde o vodorovné členění na stejné úseky c, nemusíme zatím dělat žádná kouzla, jelikož zobrazovací rovina se dotýká rohu našeho objektu, a jak již víme z 1.dílu, v tomto případě délka úseku c se v perspektivě nemění.
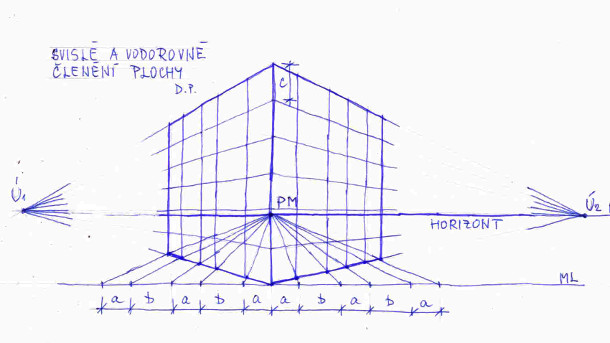
Techniku dělení si teď z cvičných důvodů aplikujeme na dlažbu (mozaiku). Na obrázku č. 9 je vysvětlen postup pro případ, že na dlažbu se díváme čelně, tedy stojíme přesně uprostřed délky a. D je tzv. distančník, což je speciální úběžník, který se využívá právě tehdy, když se opakují určité úseky, což v případě dlažby platí. Nejprve si nakreslíme v jednoúběžníkové perspektivě plochu, do které chceme dlažbu zakreslit. Pravý dolní roh spojíme s bodem D. Tam kde tahle přímka protíná přímky vedené do úběžníku Ú, vyneseme vodorovné přímky dlažby. Zde spodní hrana dlažby tvoří měřicí přímku ML z předchozího obrázku. Pokud bychom chtěli v dlažbě pokračovat, opět spojíme pravý dolní roh ještě nevydlážděné plochy s D a další postup zopakujeme.
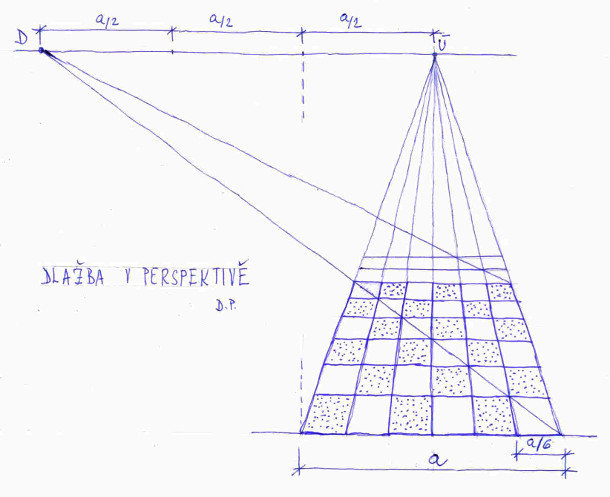
Na obrázku č. 10 je dlažba nakreslena v dvouúběžníkové perspektivě. Bod D dostaneme tam, kde úhlopříčka plochy, kterou chceme vydláždit, protne horizont. Na něm leží i měřicí bod PM. Další postup již jenom opakuje postup z obrázků č. 8 a č. 9.
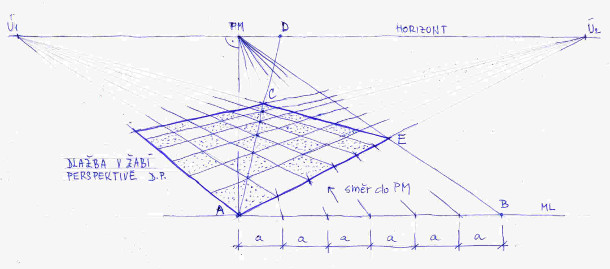
Ovšem nikdo není dokonalý, což platí i pro náš postup na předchozím obrázku. Zatím jsme plochu, kterou chceme vydláždit, kreslili tak trochu kvalifikovaným odhadem, což není nic trestuhodného, tak běžně malíři pracují. Ovšem abychom do našeho postupu přidali i trochu exaktnosti, vysvětlíme si, jak zkontrolovat, zda jsme zmíněnou plochu nakreslili perspektivně správně a navíc budeme pracovat s dvěma úběžníky. Jelikož jak úběžníků, tak i distančníků není nikdy dost. Určitě si vzpomenete na Thaletovu větu z geometrie na základní škole. Praví, že všechny úhly vytvořené na obvodu kružnice nad průměrem kružnice jsou pravé, a právě téhle zákonitosti využijeme. Sledujte pozorně obrázek č. 11. Představte si že bod O (oko pozorovatele) je o něco níž, než je tomu na obrázku. Kdybychom tento nový bod O spojili s úběžníky F1 a F2 (časté označení úběžníků v anglické literatuře), zjistili bychom, že úhel F1OF2 není pravý, jelikož neleží na obvodu námi nakreslené kružnice se středem v S, což je polovina vzdálenosti F1F2. Co by z toho pro nás plynulo? Pokud jsme správně odhadli distanci, tedy polohu bodu O, musí být nesprávně určen jeden z úběžníků F1, F2. Jak to napravíme? Musíme se rozhodnout kterou stranu ze stran AF1, AF2 budeme považovat za správnou. Ať jsme si jisti, že je to AF2. Poté naneseme pravý úhel nad úsečkou F2O v bodě O, ten nám v našem případě protne horizont v bodě F1, který bude blíž k F2. No a tím je správně stanovena poloha F1. Následně provedeme opravu. Tento postup doporučuji si dobře zapamatovat a využívat je pro korekci polohy odhadnutých úběžníků. Další postup kreslení dlažby by už měl být zřejmý z obrázku. Pro dělení plochy v tomto případě využíváme dvou distančníků D1 a D2. D3 nám může posloužit pro kontrolu správnosti nakreslení dlažby. Pochopitelně lze postupovat i jinak, a to pouze s použitím D1, nebo D2 a poté D3.
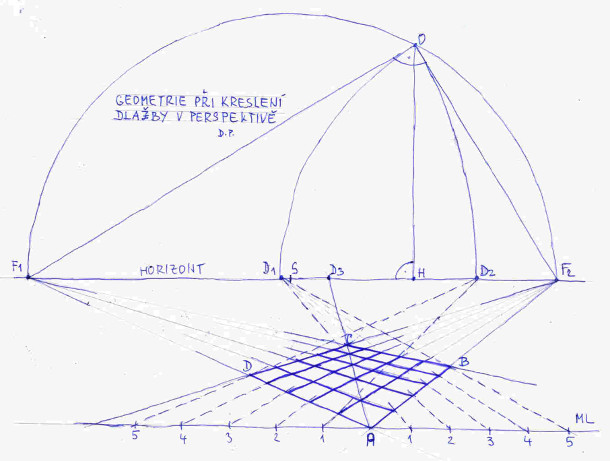
A konečně se dáme do kreslení schodů. Na obrázku č. 12 vidíme schody nakreslené v dvouúběžníkové perspektivě při čelném pohledu. Je zajímavé, že jsme si vystačili pouze s výškou schodů, přitom z praxe víme, že výška a šířka jednoho schodu nejsou obvykle stejné. Výška je obvykle výrazně menší než šířka, to kvůli pohodlné chůzi. Tohle musíme v dalším zohlednit.
Na obrázku č. 13 již pracujeme s rozdílnou výškou a šířkou jednotlivého schodu a hned to vypadá lépe, tedy realističtěji.
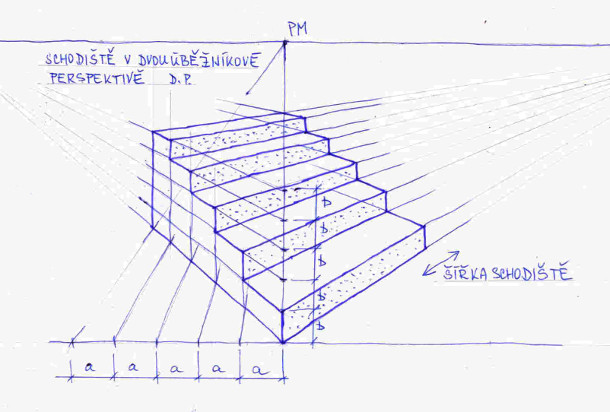
Obrázek č. 14 je velice podobný obrázku č. 13, jenom pohled na schody je jiný, což nám dovoluje vystačit si s jedním ůběžníkem.
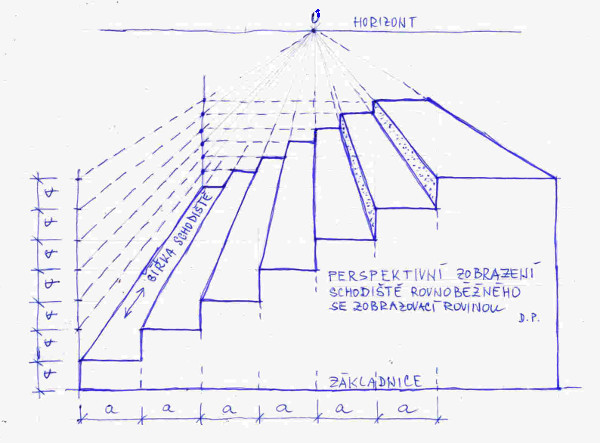
Na obrázku č. 15 jsou schody, které ubíhají a klesají od nás. Distančník D je zvolen sice „od oka“, ale tak, aby perspektiva schodů na nás působila dojmem opravdovosti.
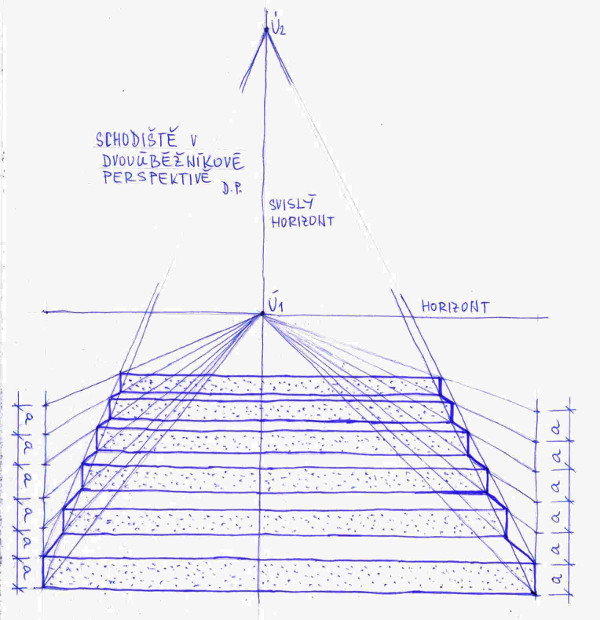
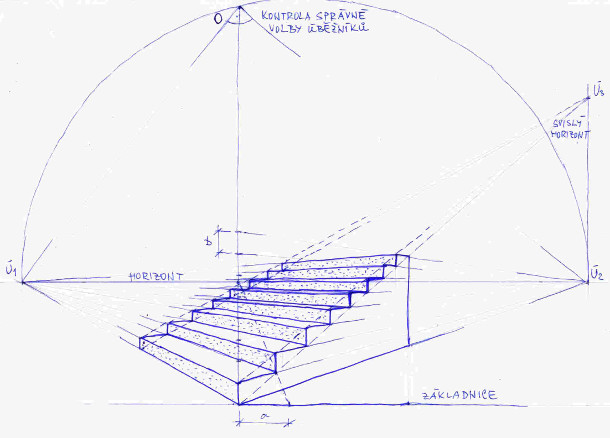
Při kreslení schodů podle obrázku č. 16 využíváme i svislý (vertikální) horizont. Právě ten nám perspektivně vymezuje vrcholy a spodky jednotlivých schodů celého schodiště. Distančník leží v průsečíku horizontu a svislice procházející čelnou stěnou prvního schodu. Použili jsme jej k určení perspektivní šířky prvního schodu. Na obrázku je zakreslena, nám již známá, kontrola správné volby úběžníků.
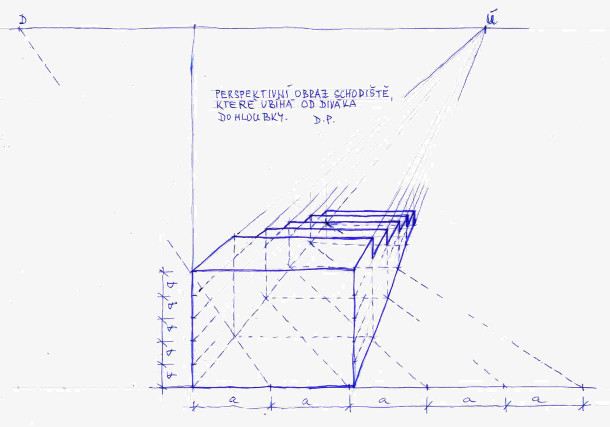
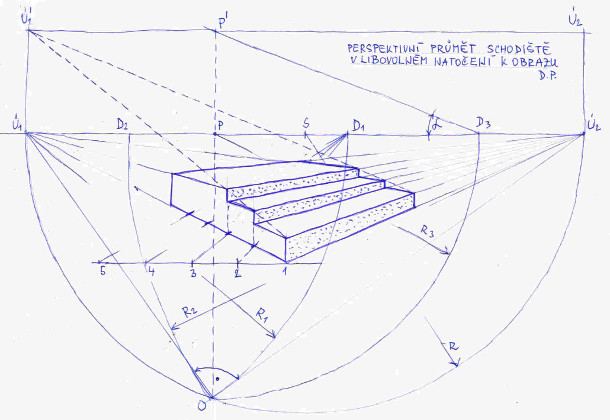
A nakonec nejdůležitější obrázek, tem má číslo 17. Zatím jsme schody kreslili více měně s citem neboli kvalifikovaným odhadem, což v praxi není až tak neobvyklé. Na tomto obrázku si vysvětlíme postup nakreslení schodů pod přesně definovaným sklonem, na obrázku je sklon označen úhlem alfa. V praxi je to vždy konkrétní hodnota v stupních. Z předchozího výkladů známe již poznáme význam distančníků D1 a D2 (ten zde nevyužíváme, je zakreslen jenom pro úplnost). Novum je distančník D3, který dostaneme vynesením kružnice se středem v bodě P a poloměrem PO. Poté z něho vyneseme úhel alfa, tedy sklon schodů. Rameno úhlu nám protne svislici vedenou body O a P v bodě P’. Pomocí tohoto bodu dostaneme průmět úběžníku Ú1 pojmenovaný Ú1’. A právě ten využijeme k vykreslení perspektivního sklonu schodů se sklonem alfa. Další postup je již jenom opakováním předchozích postupů. Jenom připomeňme, že výška prvního schodu v bodě 1 je skutečnou výškou schodu, jelikož zobrazovací rovina se dotýká svislé hrany prvního schodu. K zakreslení perspektivních šířek schodů jsme použili distančník D1.
A to je pro tentokráte vše. Příště si vysvětlíme a ukážeme jak na stíny.
V Brně 25. října 2020.
Zde je odkaz na první díl seriálu.
Zde je odkaz na třetí díl seriálu.