Něco málo o lineární perspektivě III

Dušan Polanský

Úvod do problematiky osvětlení

V třetím, posledním, díle našeho elementárního povídání o lineární perspektivě si něco povíme o kreslení stínů. Ze zkušenosti víme, že stín vrhá každý osvětlený objekt. Navíc přitom vytváří ještě vlastní stín. Ten se tvoří na těch plochách objektu, které neosvětluje zdroj světla.

Na snímku schodiště vidíme hned tři vržené stíny: můj stín vržený při focení, stín vržený zábradlím a stín vržený budovou od naproti. Přesto, že jsou to tři různé vržené stíny, mají jednu vlastnost společnou: směřují do jednoho úběžníku. Zde je slunce někde za mými zády. Snímek by určitě vypadal jinak, kdyby bylo přede mnou, nebo kdyby sluneční paprsky dopadaly rovnoběžně s fasádou domu. Je jasné, že tyto tři případy směru dopadu slunečních paprsků musíme při kreslení vržených stínů rozlišovat. Nakonec i proto prosluněné stavební pozemky jsou obvykle nejdražší (už ani nemluvě o případu, kdy je hezký výhled na okolní krajinu), u nich totiž až tak nezáleží na postavení slunce na obloze v průběhu dne. Pokud architekt chce svůj návrh dokumentovat i světelnými poměry, měl by seriózně zvolit ten případ, který je z hlediska vytvoření si představy o osvětlení stavby nejtypičtější. Tedy ani ne ten nejhorší, ale ani ne ten nejlepší.

Další obrázek nám dokumentuje pestrost intenzity osvětlení na běžném snímku z listopadu kolem 11 hodin dopoledne. Zde můžeme vidět, proč umělečtí malíři příliš veliké rozdíly mezi osvětlením a stíny nemilují, jsou totiž poměrně technicky náročné na pravdivé zachycení.

Dokladem této nesnadnosti je i tahle ne moc povedená pohlednicová reprodukce obrazu, na němž se výtvarný umělec snaží kromě truchlivé atmosféry zachytit i průnik slunečního světla malým oknem do tmavé místnosti. Autorem je malíř a ilustrátor Emanuel Krescenc Liška (1852 -1903). Pokud se chcete o jeho díle dozvědět více, stačí zadat do vyhladávače jeho jméno.

Dříve než si vysvětlíme hlavní zázady kreslení stínů v lineární perspektivě, povíme si něco málo o rovnoběžném osvětlení bez respektování perspektivní názornosti, někdy se mu také říká technické osvětlení. Na názorném obrázku č. 18 vidíme, jak vzniká vržený stín při tomto typu osvětlení. Vlastní stín sice není zde zakreslen, ale z názoru je zřejmě, že se vytvoří na plochách BCV a CDV, protože na tyto plochy světelné paprsky nedopadají. Dodejme, že u technického osvětlení se obvykle předpokládá, že světelný paprsek doapda zleva (představte si jej ve směru úhlopříčky krychle), a že průměty tohoto paprsku do půdorysny i nárysny svírají s osou x úhly 45 stupňů, tedy že to jsou úhlopříčky čtverce v půdorysně a v nárysně.

Na obrázku č. 19 je vidět způsob konstrukce vrženého stínu způsobeného čtyřbokým jehlanem při rovnoběžném osvětlení. Kvůli větší názornosti jsme použili tzv. kosoúhlé (po staru šikmé) zobrazení, kdy osa Y svírá s osou X nejčastěji úhel 135 stupňů (popravdě já osu Y frknul od oka). Abychom získali vržený stín, stačí, když budeme znát jeden vrchol vrženého stínu na rovinu XY, nechť je to např. bod C_s. Tím, že spojíme bod C₁, což je průmět vrcholu C do roviny XY, s bodem C_s, dostaneme směr vrženého stínu. Další postup je již nabýledni. Dodejme, že směr osvětlení jsme zvolili dle doporučení 45 stupňů, přičemž světelné paprsky dopadají zleva.

Tímto obrázkem s rovnoběžným osvětlením bez respektování perspektivní názornosti končíme. V dalším si budeme povídat o konstrukci stínů v lineární perspektivě, tedy budeme vycházet z toho, že vše bude směřovat do úběžníků, což bude o něco složitější než při rovnoběžném osvětlení.

Úvod do osvětlení v lineární perspektivě

Princip co nejrealističtějšího zobrazení stínů v lineární perspektivě vychází z, nám již známého, pravidla, že téměř vše musí směřovat do úběžníků. Tedy nejen hrany objektů, ale i osvětlení a stínů. Na obrázku č. 19a je názorně vidět princip tvorby stínu při respektování perspektivní názornosti. Zde je zakreslen stín svislé roviny ABCD. Stín je určen buď stínem některé svislé přímky, např. AB, nebo úběžníkem stínů a úběžníkem světelných paprsků. Vidíme že úběžníky leží na stejné svislici. Do úběžníku K směřují vodorovné přímky roviny i stínu. O rovnoběžném zobrazení mluvíme i zde, jelikož světelně paprsky dopadají z velké dálky, na našem obrázku by se jednalo o sluneční paprsky, takže představa rovnoběžnosti paprsků je na místě. Ovšem efektu názornosti dosahujeme právě díky perspektivě.

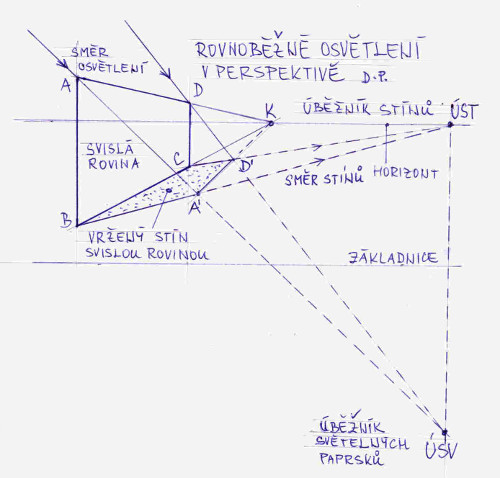
Vidíme, že celý fígl je v určení úběžníku osvětlení a úběžníku stínů. Další postup již bude jednoduchý: určíme průsečíky paprsků osvětlení a stínů jednotlivých hran. Názorně si to ukážeme na osvětlení místnosti bodovým svítidlem, viz názorný obrázek č. 20. V tomto případě za předpokaldu, že krychle má větší rozměr, již nelze mluvit o rovnoběžném zobrazení. Zde určení obou úběžníků není až tak těžké. Úběžník osvětlení je žárovka svítidla a úběžník stínů dostaneme na průsečíku vertikály spuštěné ze zdroje světla a čárkované čáry. Při konstrukci čárkované lomené čáry si stačí uvědomit, že na stropě a podlaze přímky směřují do úběžníků, do kterých směřují i obrysy stěn místnosti a pochopitelně i jednotlivé plochy nám již dobře známé krychle.

Na obrázku č. 21 je technická realizace postupu z obrázku č. 20 s tou obměnou, že světlo necháme dopadat na krychli zleva. Krychli v průčelné poloze již umíme nakreslit z minulých dílů. Stačí k tomu vhodně zvolit úběžníky F₁ a F₂ a znát velikost hrany krychle. Průmět svítidla na podlahu je dán bodem SV₁. Výškové umístění svítidla nad podlahou je dáno vzdálenosti od dolní hrany krychle v nárysu po bod SV₂. Nejprve určíme na základnici bod 5, v kterém naneseme výšku svítidla. Na svislici v bodě 6 se nám zobrazí výška svítidla v lineární perspektivě. Abychom ji získali, vedeme z bodů SV₁ a SV₂ paprsky do úběžníku F₁. Kde protnou svislici, tam získáme úběžníky osvětelení a stínů. SV₂’ je úběžník světelných paprsků, SV₁’ paprsků stínů. Vlastní obrysy stínu získáme naprosto stejnou konstrukcí jako na obrázku č. 20.

Jenomže jak najít úběžník osvětlení při slunečném osvětlení, když naše zobrazovací rovina, tedy plocha výkresu, není obvykle dostatečně veliká, abychom dokázali úběžník osvětlení najít přímo? A navíc slunce může být před námi, za námi a třetí možnost je, že sluneční paprsky dopadají zboku, tedy rovnoběžně se zobrazovací rovinou. Předchozí postup nelze mechanicky aplikovat, musíme si poradit jinak.

Jak, to nám ukáže názorný obrázek č. 22. Budeme postupovat metodou kvalifikovaného odhadu. Všimněme si v levé části obrázku zkušební tyče UV, klidně to může být rovný klacík. Tyč nám v okamžiku naší umělecké tvorby vrhá stín pod úhlem alfa. Pod tímto úhlem si myslíme nakreslenou rovnoběžku z bodu O, tedy našeho oka, směrem k slunci. Táto rovnoběžka protne zobrazovací rovinu v pomyslném bodě S. Pomyslném proto, že vůbec nemusí protnout plochu našeho výkresu. Z bodu S vedeme kolmici na horizont, čímž získáme bod SF. Pomocí tohoto bodu již snadno nakreslíme perspektivu vrženého stínu perspektivního obrazu tyče UV. Na našem obrázku perspektivním obrazem tyče UT je úsečka U’T’.

A teď praktická konstrukce pro případ, že slunce je před námi, viz obrázek č. 23. Místo označení S jsem zde použil SV, což je detail. Směr dopadu slunečních paprsků promítnutý na základní rovinu je dán směrem s, ten jednoduše odhadneme. Kde paprsek v tomto směru protne základnici, dostaneme bod SVF₁. Od tohoto směru si naneseme příslušný úhel dopadu. V praxi se obvykle volí od 40 do 45 stupňů. Jenom 35 stupňů jsem volil proto, neboť jsem chtěl aby se mi vše nějak rozumně vešlo na papír A4. Na průsečíku ramena úhlu o velikosti 35 stupňů a kolmice na přímku O₁VF₁ dostaneme bod SVF₁, který vymezuje bod, v kterém sluneční aprsky protínají zobrazovací rovinu. Na horizontu v bodě SVF, což je úběžník stínů, vyneseme na kolmici výšku h, čímž získáme úběžník světla. Vlastní konstrukce stínu je již jenom opakováním předchozích postupů.

V případě, že slunce nám svítí na záda, dopadne to nějak podobně jako je uvedeno na obrázku č. 24. Jediná změna je, že úběžník osvětlení SV je na opačné straně než na obrázku číslo 23.

Zbývá nám vysvětlit konstrukci stínu, když sluneční paprsky dopadají rovnoběžně se zobrazovací rovinou. Protože přímky rovnoběžné se zobrazovací rovinou nemají společný úběžník a promítají se v lineární perspektivě na zobrazovací rovinu opět rovnoběžně, kostrukce stínu je dána obrázkem č. 25. Úhel dopadu slunečních paprsků je dán úhlem alfa vztaženým vůči základnici.

A to je vše. Pokud vás povídání o lineární perspektivě zaujalo, doporučuji si doplnit další teorii z odborné literatury a pak hlavně kreslit, jelikož jedině cvik děla opravdového mistra.

Použitá a doporučená literatura s krátkým (já) komentářem:

• [1] Cibulka, V. Odborné kreslení pro 1. a 2. ročník SPŠS, SNTL, Praha, 1980, 196 stran.
• [2] Sýkora, J. Odborné kreslení pro SPŠ stavební, GRADA, Praha, 2011, 120 stran.
• [3] Parramón, J. M. Perspektiva pro výtvarníky, JAN VAŠUT, Praha, 1998, 112 stran.
• [4] Kochman, J., Menšík, M., Schmidt, O. Technické kreslení pro I. a II. ročník středních uměleckoprůmyslových škol, Státní pedagogické nakladatelství, Praha, 1984, 182 stran.
• [5] Civardi, G. Perspektiva, jak zobrazovat objemy a tvary, SVOJTKA&Co., Praha, 2014, 64 stran.
• [6] Kargerová, M. Deskriptivní geometrie pro technické školy vysoké, vyšší a střední, MONTANEX, Ostrava, 1997, 186 stran.
• [7] Arcas, S., Gonzales, I., Arcas, F. La Perspective, EDITICIONS PLACE DES VICTOIRES, Paris, 2009, 176 stran.
• [8] Chalupníček, B. Základy perspektivy lineárné, Nákladem ČESKÉ MATICE TECHNICKÉ, Praha, 1913, 116 stran + 24 tabulí.
• [9] Bém, F.X. Katechismus perspektivy, Nakladatel K. AUSOBSKÝ, Č. Budějovice, 1946, 62 stran.
• [10] Kupčáková, M. Základní úlohy deskriptivní geometrie v modelech, Prometheus, Praha, 2002, 64 stran.
• [11] Schmidt, R. Perspektive Schritt für Schritt, BAUVERLAG, Berlin, 1988, 104 stran.
• [12] Ritschl, B., Rischlová-Vaněčková, B. Deskriptivní geometrie v praksi, Česká grafická unie, 1938, Praha, 64 stran textu + 49 tabulí.
• [13] Barišnikov, A. P. Jak používat pravidel perspektivy při kreslení podle skutečnosti, ORBIS, Praha, 1955, 80 stran.
• [14] Smith, R., Wright, M. Horton, J. Škola kreslení a malování, SLOVART, Bratislava, 2003, 480 stran.
• [15] Morschek, K-H. Krok za krokem perspektiva, ANAGRAM, Ostrava, 2005, 32 stran.
• [16] Ritschl, B., Rischlová-Vaněčková, B. Deskriptivní geometrie v praksi stavitele, PRÁCE, raha, 1950, 232 stran.
• [17] Setzer, O. Deskriptivní geometrie II, SNTL, Praha, 1980, 176 stran.

Komentář k literatuře:

• Titul [1]. Je určen především stavařům a architektům. Je to naše klasika. Používala se k výuce již v letech 1967 až 1971, kdy jsem studoval stavební průmyslovku v Bratislavě, kde autor byl můj učitel, no a já ne příliš usilovný žák. Jak jsem již uvedl, na konci knihy jsou zadání příkladů k procvičení prostorové představivosti. Jsou zde uvedeny půdorysy a nárysy (případně bokorysy) objektů, který máte zakreslit nejlépe do perspektivní krychle. Pokud se chcete živit jako architekt nebo i realistický výtvarník, tahle cvičení vřele doporučuji.
• Titul [2]. Je takový minimax pro průmyslováky stavaře. Je poznat, že autor má za sebou dlouholetou učitelskou praxi a nezatěžuje středoškolské studenty zbytečnými detaily.
• Titul [3]. Doporučuji jej nejen všem výtvarníkům. Text je čtivý a postupy jsou pečlivě okomentovány.
• Titul [4]. Perspektivě je zde věnováno sice jenom 14 stran, ale toho nejdůležitějšího.
• Titul [5]. Je poznat, že autor je vynikající kreslíř. Vhodné pro výtvarníky.
• Titul [6]. Vhodné pro pochopení teoretického základů středového promítání a lineární perspektivy, tomuto je celkem věnováno 16 stran.
• Titul [7]. Původně španělský titul, zde je uveden francouzský překlad. Hlavně pro výtvarníky.
• Titul [8]. Text pro vysokoškoláky stavaře a studenty oboru geometrie. Dost náročný na čtení, ale obsahuje hodně teoretických poznatků. Dnes již těžko sehnatelný.
• Titul [9]. Příjemný spisek pro pochopení elementárních základů perspektivy.
• Titul [10]. Perspektivě je věnováno 5 stran textu, z toho 2 strany cylindrické perspektivě. V příloze 2 perspektivní modely. Zajímavý výklad základů perspektivy.
• Titul [11]. Vysoká pedagogická úroveň, ale bohužel v němčině. Určeno vysokoškolákům stavařům.
• Titul [12]. Kvalitní hutný text, který se věnuje i jiným druhům perspektivy. Vhodné pro stavaře a studující oboru geometrie.
• Titul [13]. Spisek vhodný pro pochopení základů lineární perspektivy.
• Titul [14]. Dílo má monografický charakter. Až po stranu 137 se věnuje různým aspektům perspektivního vidění. Vhodné především pro výtvarníky, už méně pro stavaře a architekty.
• Titul [15]. Spisek pro pochopení základů lineární perspektivy. Určeno pro výtvarníky.
• Titul [16]. Perspektivě je věnováno 25 stran hutného textu a obrázků.
• Titul [17]. Centrálnímu promítání a perspektivě je věnováno celkem 54 stran hutného textu a obrázků. V seznamu literatury jsou uvedeny i další tituly se vztahem k lineární perspektivě.

V Brně 17. listopadu 2020.

Zde je odkaz na první díl seriálu.

Zde je odkaz na druhý díl seriálu.

Domů | Prolog 2001: Vesmírná odysea | Nejen básně v próze | Střípky