Důkazy neboli permutace názorně a lehce
Dušan Polanský
S důkazy jsou problémy nejen v justiční praxi či při nenávistných a urputných bojích o majetek, ale i v běžném životě. Snad proto, že slova lze těžko ve světě, kde se lže, jak když tiskne, považovat za hodnověrný důkaz. Proto se moc nedivme, že ženy tak často naléhají na muže, aby si je vzali, a tím jim podali jasný důkaz, že jim nejde jenom o pohodlný sex, neboli moderně, kultivovaně řečeno jenom o přátelský vztah. Muži často kličkuji řečmi, že sňatek je vlastně jenom o kusu úředního papíru, jenž opravdovou lásku i tak nemůže garantovat, přitom ale dobře ví, že manželství je především závazek a odpovědnost vůči partnerovi případně časem i dětem. Někdy, ale ne často, se stává, že se karta obrátí. Důkaz chce po ženě muž. Obvykle v podobě potomka, čímž má dáma jasně prezentovat, že to myslí s dotyčným vážně a že s ním nechodí jenom proto, že momentálně lepší partie po ruce není. Muž asi tuší, že jakmile bude po ruce někdo lepší, dáma si již lehce důvod pro rozchod najde. Někdo namítne, že rozvodů i v rodinách s dětmi je dnes více než požehnaně. Jistě, ale s dítětem nebo dětmi je to podstatně komplikovanější. Jednoduše řečeno v reálném životě řečičky nikdy nebyly, nejsou a ani nebudou důkazem, neboť je to proti lidské povaze. Něco takového jako láska bez podmínek se vyskytuje především v literatuře a filmech či hrách o lásce. Vzácně se vyskytuje i v životě, ale je to obvykle jenom tedy, když jsou oba partneři na tom spíš bídně než dobře, takže láska je to jediné, co je lehce k mání.
Příběhů o různých důkazech v běžném lidském životě by se dalo vyprávět asi požehnaně. Sám několik znám, ale určitě i nejeden čtenář by mohl uvést příklad či příklady ze svého života nebo svého okolí. Leč neničme si zbytečně zrak čtením něčeho, co je často nejen fádní, ale někdy se člověku přímo ekluje. Dnes vás raději opět pozvu do světa jednoduché matematiky, ale i v té bohužel platí, že bez jasného důkazu ani rana. Výhodou je, že matematický důkaz obvykle nikomu neublíží. Jaké znalosti k našemu výletu budeme potřebovat? Bohatě vystačíme se znalostmi ze základní školy. Mezi námi, když se něco do hloubky opravdu umí, dá se téměř všechno jasně vyložit nejen v matematice, ale i v jiných vědách, pomocí znalostí ze základní školy, akurát výklad zabere hodně času a místa.
Než se dostaneme k našemu jednoduchému příkladu, malý prolog. Typů matematických důkazů je několik. V střípku Geometrická řada neboli záliba trochu jinak jsme si ukázali tzv. konstruktivní důkaz, tj. tím, že jsme něco dokázali, současně jsme našli i návod, jak to prakticky podle vzorečku vypočítat. Ovšem jsou i důkazy nekonstruktivní, tj. to, co se má dokázat nebo vyvrátit, se dokáže, že to možné je, nebo není, ale samotný důkaz vám v případě, že to možné je, návod k praktickému výpočtu toho, co bylo dokázáno, že možné je, nedává. Klasickým otřepaným příkladem je důkaz Nielse Henrika Abela o neřešitelnosti rovnic pomocí radikálů pátého a vyššího stupně s racionálními koeficienty. Pro představu o pojmu radikál stačí, když si alespoň přibližně vzpomenete na vzoreček pro řešení kvadratické rovnice, tak tá je řešitelná pomocí radikálů neboli po našem odmocnin. To ale neznamená, že nejsou speciální rovnice např. pátého stupně, které nelze řešit pomocí radikálů. Další geniální matematik Evarist Galois vymyslel, jak určit, zda konkétní rovnice pátého či vyššího stupně je, nebo není řešitelná pomocí radikálů. Jenomže tím, že podle jeho postupu dokážeme, že konkrétní rovnice např. pátého stupně je řešitelná pomocí radikálů, nemáme vůbec vyhráno, neboť neznáme postup, jak řešení rovnice napsat. Jenom víme, že to jde. Takže si musíme začít mordovat hlavu, jak tu zatracenou rovnici vyřešit. V střípku Maturita a třetí odmocnina z jedné jsme si jedno řešení speciální rovnice pátého stupně ukázali.
Dnes si ukážeme na výpočtu počtu permutací n prvků. tzv. rekurzivní typ důkazu. Co to vůbec permutace je? Není to nic jiného než uspořádání n prvků všemi možnými způsoby. Dále budeme uvažovat jenom různé prvky. Prvky si budeme dle zvyku označovat a, b, c, d, e … Začneme jedním prvkem: a. S tím ale moc zázraků neuděláme, jediná permutace je samotný prvek a. U dvou prvků: a, b to začíná být zajímavější, máme dvě permutace: ab, ba. Ze tří prvků: a, b, c dokážeme vykouzlit 6 permutací: abc, acb, bac, bca, cab, cba. Jak jsme permutace ze tří prvků vytvářeli? Každý prvek ze tří prvků jsme dali na první pozici a zbylé dva prvky jsme permutovali všemi možnými způsoby. Kvůli názornosti a přehlednosti jsme při zápisu permutací dodržovali pořadí písmen v české abecedě. Teď bychom již hravě dokázali vytvořit permutace ze čtyř prvků: a, b, c, d. Opět bychom každý prvek dali na první pozici a zbývající tři prvky bychom permutovali. Dokonce podle našeho postupu dokážeme i vypočíst počet permutací ze čtyř prvků, je to 4.6 = 24. Proč? Každý prvek na první pozici, to je ta 4, a ze zbývajícíh třech prvků se pokaždé vytvoří 6 permutací. Zkusme si teď na základě našich znalostí dokázat počet permutací pro n prvků. Předpokládejme, že známe počet permutací pro n – 1 prvků, označme tento počet Pn-1. Počet permutací z n prvků pak bude Pn = n. Pn-1, viz příklad výše z třemi a čtyřmi prvky. Je to docela zajímavý vzoreček, říká nám, že počet permutací n prvků vypočteme velice jednoduše, stačí vynásobit číslo n počtem permutací n – 1 prvků. Takže prakticky vzato, stačí nám znát počet permutací pro jeden prvek, tj. P1 a počet permutací pro vyšší počet prvků již lehce pomocí násobení vypočítám. Přesvědčme se o tom.
| P2 | = | 2.P1 |
| P3 | = | 3.P2 |
| .... | = | ....... |
| Pn-1 | = | (n-1).Pn-2 |
| Pn | = | n.Pn-1 |
Když vynásobíme levé a pravé strany všech těchto rovnic, dostaneme rovnici:
P2.P3.P4.....Pn-1.Pn = 2.3.4.....(n-1).n.P1.P2.P3.....Pn-2.Pn-1
Obě strany rovnice můžeme krátit výrazem P2.P3.....Pn-2.Pn-1, a protože P1 = 1 konečně obdržíme hledaný počet permutací z n různých prvků:
Pn = 1.2.3.4.....(n-1).n.
Asi již víte, že výraz 1.2.3.4.....(n-1).n, tj. součin všech celých kladných čísel až do n, nazýváme faktoriálem n a značíme jej zkratkou n!. Faktoriál n! roste velice rychle. 1! = 1; 4! = 24; 5! = 120; 10! = 3628800, takže vypsat explicitně všechny permutace u 10 prvků by nám dalo pěkně zabrat. My ale budeme skromni, na ukázku si v dalším vypíšeme všechny permutace ze 4 různých prvků. Pochopitelně mohli bychom při výpisu permutací postupovat zcela náhodně, ale takový postup je pracný a chybí mu systematičnost. Proto si permutace ze 4 prvků vypíšeme třemi různými systematickými postupy. Než se ale do toho dáme, dlužím vám vysvětlení, proč náš důkaz počtu permutací z n prvků byl rekurzivní.
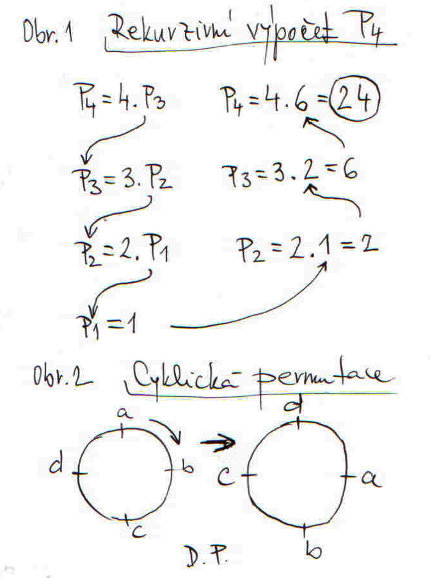
Vše si vysvětlíme na obrázku č. 1, obrázek č. 2 si zatím nevšímejte. Rekurze znamená volání stejného výrazu či stejné funkce při výpočtu stejného výrazu či stejné funkce. Ano, je to jako když si had polyká svůj ocas. Kupříkladu chci vypočíst P4, vzoreček mi říká, že P4 = 4. P3, takže musím znát P3, ale k jeho výpočtu zase potřebuji znát P2. A zase se vše opakuje, neboť k výpočtu P2 potřebuji znát P1. Teď si již konečně mohu oddechnout, neboť vím, že P1 = 1. Teď již mohu vypočíst P2, z P2 zase P3, z P3 nakonec hledaný počet permutací pro čtyři prvky P4. Pokud vás rekurze zaujala, zkuste se přečít ještě můj článek: Rekurze pro úplné začátečníky. Jinak rekurzivní výpočty se hodně využívají kupříkladu v umělé inteligenci.
V dalším si ukážeme jak všechny permutace vypsat. Ukážeme si tři postupy, vždy na 4 prvcích. U více prvků by postupy byly stejné, jenom vypsání všech permutací by nám trvalo déle.
První postup bude vycházek z přístupu popsaného při našem důkazu počtu permutací z n prvků. Výsledek vidíte v první tabulce. Připomeňme si postup z důkazu. Každý sloupec má stejný první prvek (písmeno) permutace. Druhý prvek (písmeno v abecedním pořadí) se opakuje vždy u dvou permutací zapsaných v sloupci pod sebou. Dva zbývající prvky se stejným prvkem na druhé pozici zaměníme, a tím jsme vyčerpali permutace začínající stejným prvkem (písmenem) uvedené v jednom sloupci.
| abcd | bacd | cabd | dabc |
| abdc | badc | cadb | dacb |
| acbd | bcad | cbad | dbac |
| acdb | bcda | cbda | dbca |
| adbc | bdac | cdab | dcab |
| adcb | bdca | cdba | dcba |
Při druhém postupu opět vyjdeme z výchozí permutací abcd. Platí, že při tvorbě dalších permutací máme povolenou jedinou operaci: záměnu dvou prvků. Takže ve výchozí permutaci zaměníme dva poslední prvky. V další permutaci opět budou zaměněny jenom dva prvky z permutace předchozí. Při záměnách budeme postupovat od konce permutace a dodržovat abecední pořadí. Vše je názorně vidět v druhé tabulce. Čteme ji po sloupcích. Jakmile se dostaneme na konec sloupce, opět zaměníme dva prvky, a tím si vytvoříme novou výchozí permutaci pro další sloupec atd. Kupříkladu na konci prvního sloupce jsem v permutaci adcb vzájemně zaměnil prvky: a b, tím jsem dostal výchozí permutaci druhého sloupce: bdca.
| abcd | bdca | cabd | dcba |
| abdc | bdac | cadb | dcab |
| acdb | bcad | cbda | dbac |
| acbd | bcda | cbad | dbca |
| adbc | badc | cdab | dacb |
| adcb | bacd | cdba | dabc |
Než si vysvětlíme další postup výpisu všech permutací, podívejte se o kousek výše na obr. č. 2. Na něm je ukázána tzv. cyklická permutace. Ve směru hodinových ručiček jsme zrotovali všechny prvky, takže z permutace abcd vznikla permutace dabc. Při další rotaci nám vznikne permutace cdab, při další bcda. Další rotace by nám již nevytvořila novou permutaci, neboť bychom se vrátili k výchozí permutaci abcd. Vidíme, že z n prvků lze vytvořit n cyklických permutací.
Jistě již tušíte, že náš další postup bude založen na použití cyklických permutací. Jak budeme postupovat? Z permutace o dvou prvcích cd cyklickou rotací vytvoříme novou permutaci dc. Přidejme k těmto dvěma permutacím na první pozici prvek b, tím vytvoříme dvě permutace o třech prvcích: bcd a bdc. Tyto dvě permutace o třech prvcích cyklicky zrotujeme. Z bcd dostaneme cyklické permutace: dbc a cdb. Z permutace bdc dostaneme cyklickou rotací další dvě permutace: cbd a dcb. Teď stačí před 6 námi vytvořených permutací dát písmeno a, a tím máme vytvořených 6 permutací začínajících písmenem a. Celý postup je opět nejlépe vidět na poslední, třetí, tabulce. Důležité si je uvědomit, že všechny permutace v prvním řádku každého sloupce jsou vytvořeny cyklickou rotací výchozí permutace abcd. Je to proto, že při tvorbě permutací nesmíme kromě cyklické permutace použít žádnou jinou operaci. Stejně jako v předchozí tabulce, kde jsme nesměli použít žádnou jinou operaci než záměnu dvou prvků.
| abcd | dabc | cdab | bcda |
| adbc | dcab | cbda | bacd |
| acdb | dbca | cabd | bdac |
| abdc | dacb | cdba | bcad |
| acbd | dbac | cadb | bdca |
| adcb | dcba | cbad | badc |
Mám za to, že ukázané postupy výpisu všech permutací nejsou souhrně popsány v žádné české matematické literatuře pro nematematiky. Pro matematiky určitě někde asi ano. Tak jsem si dal malou práci a udělal to za matematiky pro nás laiky nematematiky. Snad srozumitelně.
V Brně 6. března 2013.